题目内容
已知集合M={x|-1<x-a<2},N={x|x2≥x},若M∪N=R,则实数a的取值范围是( )
| A、(-1,1) |
| B、[-1,1) |
| C、[-1,1] |
| D、(-1,1] |
考点:并集及其运算
专题:集合
分析:利用不等式性质和并并集运算求解.
解答:
解:∵M={x|-1<x-a<2},N={x|x2≥x},
∴M={-1+a<x<2+a},N={x≤0或x≥1},
∵M∪N=R,∴-1+a≤0,或2+a≥1,
解得-1≤a≤1.
故选:C.
∴M={-1+a<x<2+a},N={x≤0或x≥1},
∵M∪N=R,∴-1+a≤0,或2+a≥1,
解得-1≤a≤1.
故选:C.
点评:本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意不等式性质的灵活运用.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 某数学爱好者设计了一个食品商标,如果在该商标所在平面内建立如图所示的平面直角坐标系xOy,则商标的边缘轮廓线AOC恰是函数y=tan
某数学爱好者设计了一个食品商标,如果在该商标所在平面内建立如图所示的平面直角坐标系xOy,则商标的边缘轮廓线AOC恰是函数y=tan| πα |
| 4 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
计算:sin315°的值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
正四棱锥P-ABCD的底面边长是2,侧棱长是
,且它的五个顶点都在同一个球面上,则此球的半径是( )
| 6 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
已知三棱锥的底面是边长为2正三角形,侧面均为等腰直角三角形,则此三棱锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
用辗转相除法求108和45的最大公约数为( )
| A、2 | B、9 | C、18 | D、27 |
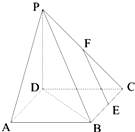 如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.
如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.