题目内容
数列{an}满足递推式an=3an-1+3n-1(n≥2),且a1=5.
(Ⅰ)求a2,a3的值;
(Ⅱ)若存在实数λ使{
}为等差数列,求λ的值及{an}的通项公式;
(Ⅲ)求{an}的前n项和Sn.
(Ⅰ)求a2,a3的值;
(Ⅱ)若存在实数λ使{
| an+λ |
| 3n |
(Ⅲ)求{an}的前n项和Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由数列{an}满足递推式分别取n=2,3,利用递推思想能求出a2,a3的值.
(Ⅱ)设
=xn+y,从而得到an=(xn+y)•3n-λ,由a1=5,a2=23,a3=95,利用待定系数法能求出λ的值及{an}的通项公式.
(Ⅲ)由an=(n+
)•3n+
,利用错位相减法能求出{an}的前n项和Sn.
(Ⅱ)设
| an+λ |
| 3n |
(Ⅲ)由an=(n+
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)∵数列{an}满足递推式an=3an-1+3n-1(n≥2),且a1=5,
∴a2=3×5+32-1=23,
a3=3×23+33-1=95.
(Ⅱ)∵{
}为等差数列,∴设
=xn+y,
∴an=(xn+y)•3n-λ,
又由a1=5,a2=23,a3=95,
知
,解得λ=-
,x=1,y=
,
∴an=(n+
)•3n+
,
∵an=(n+
)•3n+
,
∴λ=
.
(Ⅲ)∵an=(n+
)•3n+
,
记Tn=(1+
)•31+(2+
)•32+…+(n+
)•3n,①
∴3Tn=(1+
)•32+(2+
)•32+…+(n+
)•3n+1,②
-2Tn=
+32+33+…+3n-(n+
)•3n+1
=
+
-(n+
)•3n+1
=-n•3n+1,
∴Tn=
n•3n+1,
∴{an}的前n项和Sn=Tn+
=
(3n+1+1).
∴a2=3×5+32-1=23,
a3=3×23+33-1=95.
(Ⅱ)∵{
| an+λ |
| 3n |
| an+λ |
| 3n |
∴an=(xn+y)•3n-λ,
又由a1=5,a2=23,a3=95,
知
|
| 1 |
| 2 |
| 1 |
| 2 |
∴an=(n+
| 1 |
| 2 |
| 1 |
| 2 |
∵an=(n+
| 1 |
| 2 |
| 1 |
| 2 |
∴λ=
| 1 |
| 2 |
(Ⅲ)∵an=(n+
| 1 |
| 2 |
| 1 |
| 2 |
记Tn=(1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴3Tn=(1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
-2Tn=
| 9 |
| 2 |
| 1 |
| 2 |
=
| 9 |
| 2 |
| 32(1-3n-1) |
| 1-3 |
| 1 |
| 2 |
=-n•3n+1,
∴Tn=
| 1 |
| 2 |
∴{an}的前n项和Sn=Tn+
| n |
| 2 |
| n |
| 2 |
点评:本题考查数列的通项公式和前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正四棱锥P-ABCD的底面边长是2,侧棱长是
,且它的五个顶点都在同一个球面上,则此球的半径是( )
| 6 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
圆心(1,-4),且过点(4,0)的圆的标准方程为( )
| A、(x-1)2+(y+4)2=25 |
| B、(x+1)2+(y-4)2=25 |
| C、(x-1)2+(y+4)2=5 |
| D、(x+1)2+(y-4)2=5 |
已知非零向量是
,
,
满足
+
+
=
,(|
|•
-|
|•
)•
=0,且2(
•
)=|
|•|
|,则由向量
,
,
构成的三角形的三个内角分别为( )
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| b |
| a |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| A、30°,60°,90° |
| B、45°,45°,90° |
| C、30°,30°,120° |
| D、60°,60°,60° |
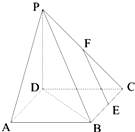 如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.
如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点.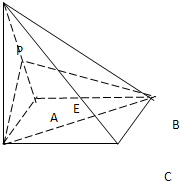 已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,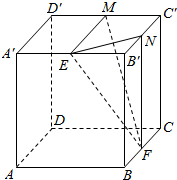 在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.
在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.