题目内容
已知复数z=
+
（m∈R）的实部是虚部的2倍，则m等于（ ）
| 1+mi |
| 4-3i |
| m |
| 25 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
考点：复数的基本概念
专题：数系的扩充和复数
分析：根据复数的基本运算，求出实部和虚部即可得到结论．
解答：
解：z=
+
=
+
=
+
=
+
+
i=
+
i，
∵实部是虚部的2倍，
∴
=2×
，
即4-2m=8m+6，
即10m=-2，
解得m=-
．
故选：C
| 1+mi |
| 4-3i |
| m |
| 25 |
| (1+mi)(4+3i) |
| (4+3i)(4-3i) |
| m |
| 25 |
| 4-3m+(4m+3)i |
| 25 |
| m |
| 25 |
=
| 4-3m |
| 25 |
| m |
| 25 |
| 4m+3 |
| 25 |
| 4-2m |
| 25 |
| 4m+3 |
| 25 |
∵实部是虚部的2倍，
∴
| 4-2m |
| 25 |
| 4m+3 |
| 25 |
即4-2m=8m+6，
即10m=-2，
解得m=-
| 1 |
| 5 |
故选：C
点评：本题主要考查复数的基本运算，利用复数的四则运算进行化简是解决本题的关键．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
某数学爱好者设计了一个食品商标，如果在该商标所在平面内建立如图所示的平面直角坐标系xOy，则商标的边缘轮廓线AOC恰是函数y=tan| πα |
| 4 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
用辗转相除法求108和45的最大公约数为（ ）
| A、2 | B、9 | C、18 | D、27 |
某高校进行自主招生，先从报名者筛选出400人参加考试，再按笔试成绩择优选出100人参加面试．现随机抽取24名笔试者的成绩，如下表所示：
据此估计参加面试的分数线大约是（ ）
| 分数段 | [60，65） | [65，70） | [70，75） | [75，80） | [80，85） | [85，90） |
| 人数 | 2 | 3 | 4 | 5 | 9 | 1 |
| A、75 | B、80 | C、85 | D、90 |
圆心（1，-4），且过点（4，0）的圆的标准方程为（ ）
| A、（x-1）2+（y+4）2=25 |
| B、（x+1）2+（y-4）2=25 |
| C、（x-1）2+（y+4）2=5 |
| D、（x+1）2+（y-4）2=5 |
若a＞b，m＞0，则下列不等式中，恒成立的是（ ）
| A、（a+m）2＞（b+m）2 | ||||
B、
| ||||
| C、（a-m）3＞（b-m）3 | ||||
| D、|am|＞|bm| |
已知非零向量是
，
，
满足
+
+
=
，（|
|•
-|
|•
）•
=0，且2（
•
）=|
|•|
|，则由向量
，
，
构成的三角形的三个内角分别为（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| b |
| a |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| A、30°，60°，90° |
| B、45°，45°，90° |
| C、30°，30°，120° |
| D、60°，60°，60° |
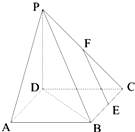如图，四边形ABCD为正方形，PD⊥平面ABCD，E、F分别为BC和PC的中点．
（1）已知角a的终边经过点P（3，-4）求：