题目内容
16.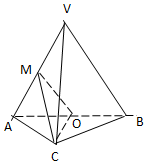 如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.(Ⅰ)求证:VB∥平面 M OC;
(Ⅱ)求三棱锥V-A BC的体积.
分析 (Ⅰ)由O,M分别为AB,VA的中点,知OM∥VB.由此能证明VB∥平面MOC.
(Ⅱ)推导出OC⊥AB,从而OC⊥平面VAB.由三棱锥V-ABC的体积与三棱锥C-VAB的体积相等,能求出三棱锥V-ABC的体积.
解答 证明:(Ⅰ)因为O,M分别为AB,VA的中点,
所以OM∥VB.
又因为VB?平面MOC,OM?平面MOC,
所以VB∥平面MOC.…(4分)
解:(Ⅱ)因为AC=BC,O为AB的中点,所以OC⊥AB.
又因为平面VAB⊥平面ABC,且OC?平面ABC,所以OC⊥平面VAB.
在等腰直角三角形ACB中,$AC=BC=\sqrt{2}$,所以AB=2,OC=1.
所以等边三角形VAB的面积${S_{△VAB}}=\sqrt{3}$.又因为OC⊥平面VAB,
所以三棱锥C-VAB的体积等于$\frac{x^2}{{3{c^2}}}+\frac{y^2}{{2{c^2}}}=1$.
又因为三棱锥V-ABC的体积与三棱锥C-VAB的体积相等,
所以三棱锥V-ABC的体积为$\frac{{\sqrt{3}}}{3}$.…(12分)
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
4.在△ABC中,$AC=\sqrt{7},BC=2,B=60°$,则BC边上的高为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $\sqrt{6}$ |
11.已知球面上的四点P、A、B、C,PA、PB、PC的长分别为3、4、5,且这三条线段两两垂直,则这个球的体积为( )
| A. | $\frac{{1000\sqrt{2}}}{3}π$ | B. | $\frac{{375\sqrt{2}}}{16}π$ | C. | 50π | D. | $\frac{{125\sqrt{2}}}{3}π$ |
1.函数f(x)满足对于任意实数x,都有f(-x)=f(x),且当x1,x2∈[0,+∞),x1≠x2时,$\frac{{f({x_1})-f({x_2})}}{{{x_1}-x}}>0$都成立,则下列结论正确的是( )
| A. | f(-2)>f(0)>f(1) | B. | f(-2)>f(1)>f(0) | C. | f(1)>f(0)>f(-2) | D. | f(1)>f(-2)>f(0) |
8.空间的一个基底{a,b,c}所确定平面的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个以上 |
5.函数y=|x|-2的图象是( )
| A. |  | B. |  | C. |  | D. |  |