题目内容
8.空间的一个基底{a,b,c}所确定平面的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个以上 |
分析 利用基底的定义以及平面的基本性质,判断即可.
解答 解:空间的一个基底{a,b,c},说明三个向量不共线,
又两条相交直线确定一个平面,
所以空间的一个基底{a,b,c}所确定平面的个数为3个.
故选:C.
点评 本题考查空间向量基底的定义,平面的基本性质,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列命题:
(1)“若am2≥bm2,则a≥b”的否命题;
(2)“全等三角形面积相等”的逆命题;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”的逆否命题;
其中正确命题的个数是( )
(1)“若am2≥bm2,则a≥b”的否命题;
(2)“全等三角形面积相等”的逆命题;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”的逆否命题;
其中正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≤0}\\{{x}^{2}+ax+1,x>0}\end{array}\right.$,F(x)=f(x)-x-1,且函数F(x)有2个零点,则实数a的取值范围为( )
| A. | (一∞,0] | B. | [1,+∞) | C. | (一∞,1) | D. | (0,+∞) |
13.化简$\frac{cos2α}{{4{{sin}^2}(\frac{π}{4}+α)tan(\frac{π}{4}-α)}}$=( )
| A. | cosα | B. | sinα | C. | 1 | D. | $\frac{1}{2}$ |
17.如图,将正方形ABCD沿对角线AC折成一个直二面角,则异面直线AB和CD所成的角是( )
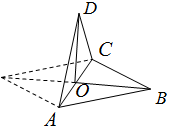

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
18.“函数f(x)=ax+3在(-1,2)上存在零点”是“3<a<4”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
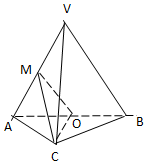 如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.