题目内容
4.在△ABC中,$AC=\sqrt{7},BC=2,B=60°$,则BC边上的高为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $\sqrt{6}$ |
分析 在△ABC中,由余弦定理可得,AC2=AB2+BC2-2AB•BCcosB可求AB=3,作AD⊥BC,则在Rt△ABD中,AD=AB×sinB.
解答 解:在△ABC中,由余弦定理可得,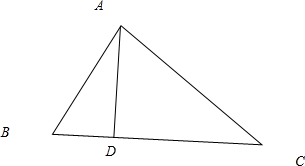
AC2=AB2+BC2-2AB•BCcosB,
把已知AC=$\sqrt{7}$,BC=2,B=60°代入可得,
7=AB2+4-4AB×$\frac{1}{2}$,
整理可得,AB2-2AB-3=0,
∴AB=3.
作AD⊥BC垂足为D,
Rt△ABD中,AD=AB×sin60°=$\frac{3\sqrt{3}}{2}$,
即BC边上的高为$\frac{3\sqrt{3}}{2}$.
故选C.
点评 本题主要考查了余弦定理在解三角形中的应用,解答本题的关键是求出AB,属于基础试题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若O为坐标原点,直线y=2b与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右两支分别交于A、B两点,直线OA的斜率为-1,则该双曲线的渐近线的斜率为( )
| A. | ±$\frac{\sqrt{5}}{2}$ | B. | ±$\frac{3}{2}$ | C. | ±$\frac{\sqrt{30}}{5}$ | D. | ±$\frac{3\sqrt{5}}{5}$ |
12.设函数f(x)=($\frac{sinB}{cosA}$)x+($\frac{sinA}{cosB}$)x,其中A、B为△ABC的内角,如果对任意x>0都有f(x)<2,那么( )
| A. | 0<A+B<$\frac{π}{4}$ | B. | 0<A+B<$\frac{π}{2}$ | C. | $\frac{π}{2}$<A+B<$\frac{3π}{4}$ | D. | A+B>$\frac{π}{2}$ |
19.下列命题:
(1)“若am2≥bm2,则a≥b”的否命题;
(2)“全等三角形面积相等”的逆命题;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”的逆否命题;
其中正确命题的个数是( )
(1)“若am2≥bm2,则a≥b”的否命题;
(2)“全等三角形面积相等”的逆命题;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”的逆否命题;
其中正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.化简$\frac{cos2α}{{4{{sin}^2}(\frac{π}{4}+α)tan(\frac{π}{4}-α)}}$=( )
| A. | cosα | B. | sinα | C. | 1 | D. | $\frac{1}{2}$ |
14.已知函数$f(x)=sin(\frac{π}{3}x+φ)(|φ|<\frac{π}{2})$的图象关于直线x=1对称,把f(x)的图象向右平移3个单位长度后,所得图象对应的函数解析式为( )
| A. | y=sin($\frac{π}{3}$x+$\frac{π}{6}$) | B. | y=sin($\frac{π}{3}$x-$\frac{π}{6}$) | C. | y=cos($\frac{π}{3}$x+$\frac{π}{6}$) | D. | y=sin($\frac{π}{3}$x-$\frac{5π}{6}$) |
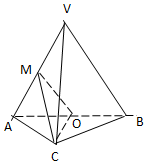 如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.