题目内容
11.已知球面上的四点P、A、B、C,PA、PB、PC的长分别为3、4、5,且这三条线段两两垂直,则这个球的体积为( )| A. | $\frac{{1000\sqrt{2}}}{3}π$ | B. | $\frac{{375\sqrt{2}}}{16}π$ | C. | 50π | D. | $\frac{{125\sqrt{2}}}{3}π$ |
分析 由题意知球面上的四点P、A、B、C是长方体的一个角,扩展为长方体,长方体的对角线就是外接球的直径,求出直径即求出外接球的体积.
解答 解:球面上的四点P、A、B、C,又PA、PB、PC的长分别为3、4、5,且这三条线段两两垂直,是长方体的一个角,
扩展为长方体,两者的外接球相同,长方体的对角线长为l=$\sqrt{9+16+25}$=5$\sqrt{2}$,外接球的半径为R=$\frac{5\sqrt{2}}{2}$;
∴球的体积为:V=$\frac{4}{3}π{R}^{3}$=$\frac{125\sqrt{2}}{3}π$.
故选D.
点评 本题考查了四面体的外接球体积的求法问题,解题时把四面体扩展为长方体,长方体的对角线就是球的直径.

练习册系列答案
相关题目
19.下列命题:
(1)“若am2≥bm2,则a≥b”的否命题;
(2)“全等三角形面积相等”的逆命题;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”的逆否命题;
其中正确命题的个数是( )
(1)“若am2≥bm2,则a≥b”的否命题;
(2)“全等三角形面积相等”的逆命题;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”的逆否命题;
其中正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.已知动点P在曲线2x2-y=0上移动,则点A(0,-1)与点P连线中点的轨迹方程是( )
| A. | y=2x2 | B. | y=8x2 | C. | $y=4{x^2}+\frac{1}{2}$ | D. | $y=4{x^2}-\frac{1}{2}$ |
3.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≤0}\\{{x}^{2}+ax+1,x>0}\end{array}\right.$,F(x)=f(x)-x-1,且函数F(x)有2个零点,则实数a的取值范围为( )
| A. | (一∞,0] | B. | [1,+∞) | C. | (一∞,1) | D. | (0,+∞) |
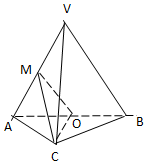 如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.