题目内容
1.函数f(x)满足对于任意实数x,都有f(-x)=f(x),且当x1,x2∈[0,+∞),x1≠x2时,$\frac{{f({x_1})-f({x_2})}}{{{x_1}-x}}>0$都成立,则下列结论正确的是( )| A. | f(-2)>f(0)>f(1) | B. | f(-2)>f(1)>f(0) | C. | f(1)>f(0)>f(-2) | D. | f(1)>f(-2)>f(0) |
分析 根据题意,分析可得函数f(x)为偶函数,进而由偶函数的性质有f(-2)=f(2),继而分析可得函数f(x)在[0,+∞)上为增函数,分析可得f(2)>f(1)>f(0),结合f(-2)=f(2),分析可得f(-2)>f(1)>f(0);即可得答案.
解答 解:根据题意,函数f(x)满足对于任意实数x,都有f(-x)=f(x),
则函数f(x)为偶函数,有f(-2)=f(2),
又由当x1,x2∈[0,+∞),x1≠x2时,$\frac{{f({x_1})-f({x_2})}}{{{x_1}-x_2}}>0$都成立,则函数f(x)在[0,+∞)上为增函数,
有f(2)>f(1)>f(0);
又由f(-2)=f(2),
则有f(-2)>f(1)>f(0);
故选:B.
点评 本题考查函数奇偶性与单调性的综合应用,关键是依据题意,分析出函数的奇偶性与单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.若函数y=f(x)在区间I上是增函数,且函数$y=\frac{f(x)}{x}$在区间I上是减函数,则称函数f(x)是区间I上的“H函数”.对于命题:①函数$f(x)=-x+2\sqrt{x}$是(0,1)上的“H函数”;②函数$g(x)=\frac{2x}{{1-{x^2}}}$是(0,1)上的“H函数”.下列判断正确的是( )
| A. | ①和②均为真命题 | B. | ①为真命题,②为假命题 | ||
| C. | ①为假命题,②为真命题 | D. | ①和②均为假命题 |
12.设函数f(x)=($\frac{sinB}{cosA}$)x+($\frac{sinA}{cosB}$)x,其中A、B为△ABC的内角,如果对任意x>0都有f(x)<2,那么( )
| A. | 0<A+B<$\frac{π}{4}$ | B. | 0<A+B<$\frac{π}{2}$ | C. | $\frac{π}{2}$<A+B<$\frac{3π}{4}$ | D. | A+B>$\frac{π}{2}$ |
6.抛物线x2=$\frac{1}{4}$y上的一点M到焦点的距离为1,则点M到x轴的距离是( )
| A. | $\frac{17}{16}$ | B. | $\frac{15}{16}$ | C. | 1 | D. | $\frac{7}{8}$ |
13.化简$\frac{cos2α}{{4{{sin}^2}(\frac{π}{4}+α)tan(\frac{π}{4}-α)}}$=( )
| A. | cosα | B. | sinα | C. | 1 | D. | $\frac{1}{2}$ |
11.一条光线从点(-2,-3)射出,经y轴反射后与圆(x+3)2+(y-2)2=1相切,则入射光线所在直线的斜率为( )
| A. | $\frac{3}{2}$或$\frac{2}{3}$ | B. | $\frac{4}{3}$或$\frac{3}{4}$ | C. | $\frac{5}{3}或\frac{3}{5}$ | D. | $\frac{5}{4}或\frac{4}{5}$ |
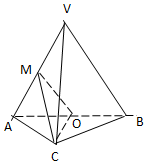 如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.