题目内容
7.马路有五个路灯,为节约用电又看清路面,可以把其中的一只灯关掉,在两端的灯不能关掉的情况下,满足条件的关灯方法有3种.分析 根据题意,分析可得需要在中间3盏路灯中选一只关掉,有组合数公式计算可得答案.
解答 解:根据题意,五个路灯中选一只灯关掉,而两端的灯不能关掉,
则需要在中间3盏路灯中选一只关掉,有C31=3种;
故答案为:3.
点评 本题考查组合数的应用,注意“两端的灯不能关掉的情况”的条件限制.

练习册系列答案
相关题目
1.若O为坐标原点,直线y=2b与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右两支分别交于A、B两点,直线OA的斜率为-1,则该双曲线的渐近线的斜率为( )
| A. | ±$\frac{\sqrt{5}}{2}$ | B. | ±$\frac{3}{2}$ | C. | ±$\frac{\sqrt{30}}{5}$ | D. | ±$\frac{3\sqrt{5}}{5}$ |
12.设函数f(x)=($\frac{sinB}{cosA}$)x+($\frac{sinA}{cosB}$)x,其中A、B为△ABC的内角,如果对任意x>0都有f(x)<2,那么( )
| A. | 0<A+B<$\frac{π}{4}$ | B. | 0<A+B<$\frac{π}{2}$ | C. | $\frac{π}{2}$<A+B<$\frac{3π}{4}$ | D. | A+B>$\frac{π}{2}$ |
19.下列命题:
(1)“若am2≥bm2,则a≥b”的否命题;
(2)“全等三角形面积相等”的逆命题;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”的逆否命题;
其中正确命题的个数是( )
(1)“若am2≥bm2,则a≥b”的否命题;
(2)“全等三角形面积相等”的逆命题;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”的逆否命题;
其中正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.如图,将正方形ABCD沿对角线AC折成一个直二面角,则异面直线AB和CD所成的角是( )
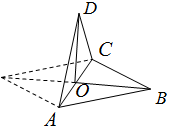

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
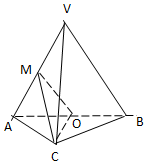 如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAV⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别AB,VA的中点.