题目内容
已知函数f(x)=(e-1)lnx-x+a(a>1).
(1)求函数f(x)的单调区间;
(2)记函数f(x)在区间[1,a]上的最小值为g(a).
(i)求g(a)的表达式;(ii)求满足g(a)=g(
)的实数a的取值集合.
(1)求函数f(x)的单调区间;
(2)记函数f(x)在区间[1,a]上的最小值为g(a).
(i)求g(a)的表达式;(ii)求满足g(a)=g(
| 4 |
| a |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)求出函数f(x)的导数,令导数对于0,得增区间,令导数小于0,得减区间,注意函数的定义域;
(2)(i)易知f(e)=f(1)=a-1,讨论当1<a≤e时,当a>e时,求出最小值;
(ii)易知g(a)在[1,+∞)上单调递增,则g(a)=g(
)即有a=
,即可求得a的值.
(2)(i)易知f(e)=f(1)=a-1,讨论当1<a≤e时,当a>e时,求出最小值;
(ii)易知g(a)在[1,+∞)上单调递增,则g(a)=g(
| 4 |
| a |
| 4 |
| a |
解答:
解:(1)函数f(x)的导数为f′(x)=
-1=
(x>0),
当0<x<e-1时,f′(x)>0,当x>e-1时,f′(x)<0,
则f(x)的单调递增区间为(0,e-1),递减区间为(e-1,+∞);
(2)易知f(e)=f(1)=a-1,
(i)①当1<a≤e时,f(x)min=f(1)=a-1,
②当a>e时,[1,a]为减区间,则f(x)min=f(a)=(e-1)lna
∴g(a)=
;
(ii)易知g(a)在[1,+∞)上单调递增,
∴g(a)=g(
)?a=
(a>1),
∴a=2,
∴满足g(a)=g(
)的实数a的取值集合为{2}.
| e-1 |
| x |
| e-1-x |
| x |
当0<x<e-1时,f′(x)>0,当x>e-1时,f′(x)<0,
则f(x)的单调递增区间为(0,e-1),递减区间为(e-1,+∞);
(2)易知f(e)=f(1)=a-1,
(i)①当1<a≤e时,f(x)min=f(1)=a-1,
②当a>e时,[1,a]为减区间,则f(x)min=f(a)=(e-1)lna
∴g(a)=
|
(ii)易知g(a)在[1,+∞)上单调递增,
∴g(a)=g(
| 4 |
| a |
| 4 |
| a |
∴a=2,
∴满足g(a)=g(
| 4 |
| a |
点评:本题考查导数的运用:求单调区间、极值和最值,考查函数的单调性的运用,考查运算能力,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
与函数y=x有相同图象的一个函数是( )
A、y=
| ||
B、y=(
| ||
| C、y=logaax(a>o,a≠1) | ||
D、y=
|
以y=±x为渐近线且经过点(2,0)的双曲线方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
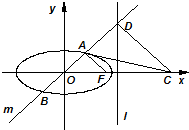 已知椭圆Γ:
已知椭圆Γ: