题目内容
函数y=
sin（
-2x）-3的单调递增区间是 ．
| 2 |
| π |
| 4 |
考点：正弦函数的单调性
专题：三角函数的图像与性质
分析：令2kπ+
≤
-2x≤2kπ+
，k∈z，求得x的范围，可得函数y=
sin（
-2x）-3的单调递增区间．根据三角函数的图象和性质即可得到结论．
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| 2 |
| π |
| 4 |
解答：
解：y=
sin（
-2x）-3=-
sin（2x-
）-3
2kπ+
≤2x-
≤2kπ+
⇒kπ+
≤x≤kπ+
，k∈Z
所以，sin（2x-
）的单调递减区间是[kπ+
，kπ+
]，k∈Z
故函数y=
sin（
-2x）-3的单调递增区间是[kπ+
，kπ+
]，k∈Z
故答案为：[kπ+
，kπ+
]，k∈Z
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
2kπ+
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| 3π |
| 8 |
| 7π |
| 8 |
所以，sin（2x-
| π |
| 4 |
| 3π |
| 8 |
| 7π |
| 8 |
故函数y=
| 2 |
| π |
| 4 |
| 3π |
| 8 |
| 7π |
| 8 |
故答案为：[kπ+
| 3π |
| 8 |
| 7π |
| 8 |
点评：本题主要考查三角函数的图象和性质，利用复合函数单调性之间的关系是解决本题的关键．
练习册系列答案
相关题目
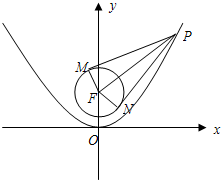已知抛物线C：x2=2py（p＞0）的焦点为F，点A（a，4）为抛物线C上的定点，点P为抛物线C上的动点．且△FOA的外接圆圆心到准线的距离为