题目内容
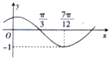函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由图象顶点坐标求得A，由周期求的ω，根据图象经过点（
，0）求得φ的值，可得函数f（x）的解析式，再根据y=Asin（ωx+φ）的图象变换规律可得结论．
| π |
| 3 |
解答：
解：由函数f（x）=Asin（ωx+φ）可得A=1，
•
=
-
，∴ω=2，
再由sin（ 2×
+φ ）=0，结合|φ|＜
可得φ=
．
∴f（x）=sin（2x+
）．
把f（x）=sin2（x+
）的图象进行左右平移使其图象关于原点中心对称，则平移的最小长度为
，
故选：B．
| 1 |
| 4 |
| 2π |
| ω |
| 7π |
| 12 |
| π |
| 3 |
再由sin（ 2×
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
∴f（x）=sin（2x+
| π |
| 3 |
把f（x）=sin2（x+
| π |
| 6 |
| π |
| 6 |
故选：B．
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，函数y=Asin（ωx+φ）的图象变换规律，属于中档题．
练习册系列答案
相关题目
集合A={x|x2-2x=0}B={-1，0，1}，则A∩B=（ ）
| A、{0，2} | B、{2} |
| C、{0} | D、{0，1} |
已知函数f（x）=|log2x|-m（m＞0）的零点分别为x1，x2（x1＜x2），函数g（x）=|log2x|-
（m＞0）的零点分别为x3，x4（x3＜x4），则
的最小值为（ ）
| 8 |
| 2m+1 |
| |x2-x4| |
| |x1-x3| |
A、4
| |||
B、8
| |||
C、4
| |||
D、8
|
已知集合M={x|
＞0}，N={x|x≤-3}，则{x|x≥1}等于（ ）
| x+3 |
| 1-x |
| A、（∁RM）∩N |
| B、M∪（∁RN） |
| C、∁R（M∩N） |
| D、∁R（M∪N） |
设f（x）是周期为4的奇函数，当0≤x≤2时，f（x）=x（2-x），则f（-5）等于（ ）
| A、1 | B、-1 | C、3 | D、-3 |
设Sn为等差数列{an}的前n项和，若a1=1，公差d=2，Sn+2-Sn=36，则n=（ ）
| A、5 | B、6 | C、7 | D、8 |
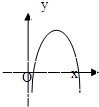
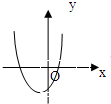
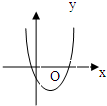
已知函数f（x）=ax3+bx2+（c-3a-2b）x+d的图象如图所示．