题目内容
设f（x）是周期为4的奇函数，当0≤x≤2时，f（x）=x（2-x），则f（-5）等于（ ）
| A、1 | B、-1 | C、3 | D、-3 |
考点：函数的周期性,函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数的奇偶性和周期性即可进行求值．
解答：
解：当0≤x≤2时，f（x）=x（2-x），
∴f（1）=1×（2-1）=1
∵f（x）是周期为2的奇函数，
∴f（-5）=-f（5）=-f（2×2+1）=-f（1）=-1．
故选B．
∴f（1）=1×（2-1）=1
∵f（x）是周期为2的奇函数，
∴f（-5）=-f（5）=-f（2×2+1）=-f（1）=-1．
故选B．
点评：本题主要考查函数奇偶性和周期的应用，综合考查函数性质的综合应用．
练习册系列答案
相关题目
已知公差不为零的等差数列{an}的首项是公差的4倍，若am是a1和a2m的等比例中项，则m=（ ）
| A、2 | B、3 | C、4 | D、5 |
设集合A={x|-
＜x＜2}，B={x|-1≤x≤1}，则A∩B等于（ ）
| 1 |
| 2 |
| A、{x|1≤x＜2} | ||
| B、{x|x＜2} | ||
| C、{x|-1≤x＜2} | ||
D、{x|-
|
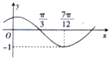函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，AC=6，BC=7，cosA=
，O是△ABC的内心，在△ABC内随机任取一点P，则取到满足条件
=x
+y
（0≤x≤1且0≤y≤1）时的点P的概率为（ ）
| 1 |
| 5 |
| OP |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={1，3，m}，B={1，
}，A∩B=B，那么m=（ ）
| m |
A、0或
| ||
| B、0或9 | ||
C、1或
| ||
| D、1或9 |
定义在实数集R函数f（x）满足f（x）+f（x+2）=0，且f（x-1）为奇函数，现有以下三种叙述：
（1）8是函数f（x）的一个周期；
（2）f（x）的图象关于点（3，0）对称；
（3）f（x）是偶函数．
其中正确的是（ ）
（1）8是函数f（x）的一个周期；
（2）f（x）的图象关于点（3，0）对称；
（3）f（x）是偶函数．
其中正确的是（ ）
| A、（2）（3） |
| B、（1）（2） |
| C、（1）（3） |
| D、（1）（2）（3） |