题目内容
已知函数f（x）=ax3+bx2+（c-3a-2b）x+d的图象如图所示．（1）求c，d的值；
（2）若函数f（x）在x=2处的切线方程为3x+y-11=0，求函数f（x）的解析式．
考点：利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题：计算题,导数的概念及应用
分析：（1）求导函数，利用函数f（x）的图象过点（0，3），且f′（1）=0，建立方程，即可求c，d的值；
（2）利用函数f（x）在x=2处的切线方程为3x+y-11=0，建立方程，即可求出a，b，从而可求函数f（x）的解析式．
（2）利用函数f（x）在x=2处的切线方程为3x+y-11=0，建立方程，即可求出a，b，从而可求函数f（x）的解析式．
解答：
解：函数f（x）的导函数为f′（x）=3ax2+2bx+c-3a-2b…（3分）
（1）由图可知，函数f（x）的图象过点（0，3），且f′（1）=0
∴
⇒
…（7分）
（2）依题意 f′（2）=-3且f（2）=5，
∴
解得a=1，b=-6，
∴f（x）=x3-6x2+9x+3…（12分）
（1）由图可知，函数f（x）的图象过点（0，3），且f′（1）=0
∴
|
|
（2）依题意 f′（2）=-3且f（2）=5，
∴
|
解得a=1，b=-6，
∴f（x）=x3-6x2+9x+3…（12分）
点评：本题考查导数知识的综合运用，考查导数的几何意义，考查函数的解析式，属于中档题．
练习册系列答案
相关题目
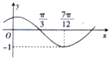函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知tanα=-
，且α为第四象限角，则cosα等于（ ）
| 3 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
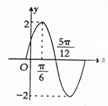已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜