题目内容
设Sn为等差数列{an}的前n项和，若a1=1，公差d=2，Sn+2-Sn=36，则n=（ ）
| A、5 | B、6 | C、7 | D、8 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由Sn+2-Sn=36，得an+1+an+2=36，代入等差数列的通项公式求解n．
解答：
解：由Sn+2-Sn=36，得：an+1+an+2=36，
即a1+nd+a1+（n+1）d=36，
又a1=1，d=2，
∴2+2n+2（n+1）=36．
解得：n=8．
故选：D．
即a1+nd+a1+（n+1）d=36，
又a1=1，d=2，
∴2+2n+2（n+1）=36．
解得：n=8．
故选：D．
点评：本题考查了等差数列的性质，考查了等差数列的通项公式，是基础题．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
如果实数x，y满足条件
，则z=2x-y的最大值为（ ）
|
| A、-3 | B、-1 | C、0 | D、1 |
已知各项都是正数的等比数列{an}中，若a3是6a1与4a2的等差中项，则
=（ ）
| a4+a7 |
| a4+a5 |
| A、7 | ||
| B、9 | ||
C、
| ||
D、
|
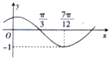函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知变量x，y满足约束条件
，则z=3x+y的取值范围是（ ）
|
| A、[3，11] |
| B、[-1，11] |
| C、[-1，9] |
| D、[-1，3] |
已知集合A={1，3，m}，B={1，
}，A∩B=B，那么m=（ ）
| m |
A、0或
| ||
| B、0或9 | ||
C、1或
| ||
| D、1或9 |
如图，E、F、G、H分别是任意四边形ABCD各边中点，若|| AB |
| BC |
| BA |
| AD |
| A、正方形 | B、梯形 | C、菱形 | D、矩形 |
已知tanα=-
，且α为第四象限角，则cosα等于（ ）
| 3 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|