题目内容
已知函数f(x)=|log2x|-m(m>0)的零点分别为x1,x2(x1<x2),函数g(x)=|log2x|-
(m>0)的零点分别为x3,x4(x3<x4),则
的最小值为( )
| 8 |
| 2m+1 |
| |x2-x4| |
| |x1-x3| |
A、4
| |||
B、8
| |||
C、4
| |||
D、8
|
考点:函数与方程的综合运用,函数零点的判定定理
专题:函数的性质及应用,不等式的解法及应用
分析:由题意求出x1,x2,x3,x4,化简所求表达式,利用基本不等式求出表达式的最小值即可.
解答:
解:函数f(x)=|log2x|-m(m>0)的零点分别为x1,x2(x1<x2),
∴x1=(
)m,x2=2m,
函数g(x)=|log2x|-
(m>0)的零点分别为x3,x4(x3<x4),
∴x3=(
)
,x4=2
,
∴
=
=
=2m•2
=2m+
=2m+
+
-
∵m+
+
-
≥2
-
=
,当且仅当m=
时等号成立,
∴2m+
+
-
≥2
=8
.
故选:D.
∴x1=(
| 1 |
| 2 |
函数g(x)=|log2x|-
| 8 |
| 2m+1 |
∴x3=(
| 1 |
| 2 |
| 8 |
| 2m+1 |
| 8 |
| 2m+1 |
∴
| |x2-x4| |
| |x1-x3| |
|2m-2
| ||||||
|(
|
|2m-2
| ||||
|2m-2
|
| 8 |
| 2m+1 |
| 8 |
| 2m+1 |
| 1 |
| 2 |
| 4 | ||
m+
|
| 1 |
| 2 |
∵m+
| 1 |
| 2 |
| 4 | ||
m+
|
| 1 |
| 2 |
(m+
|
| 1 |
| 2 |
| 7 |
| 2 |
| 3 |
| 2 |
∴2m+
| 1 |
| 2 |
| 4 | ||
m+
|
| 1 |
| 2 |
| 7 |
| 2 |
| 2 |
故选:D.
点评:本题考查函数与方程的综合应用,函数的零点以及基本不等式的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
执行如图所示的程序框图,若输出的n=5,则输入整数P的最小值是( )


| A、7 | B、8 | C、15 | D、16 |
已知公差不为零的等差数列{an}的首项是公差的4倍,若am是a1和a2m的等比例中项,则m=( )
| A、2 | B、3 | C、4 | D、5 |
已知各项都是正数的等比数列{an}中,若a3是6a1与4a2的等差中项,则
=( )
| a4+a7 |
| a4+a5 |
| A、7 | ||
| B、9 | ||
C、
| ||
D、
|
设集合A={x|-
<x<2},B={x|-1≤x≤1},则A∩B等于( )
| 1 |
| 2 |
| A、{x|1≤x<2} | ||
| B、{x|x<2} | ||
| C、{x|-1≤x<2} | ||
D、{x|-
|
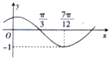 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={1,3,m},B={1,
},A∩B=B,那么m=( )
| m |
A、0或
| ||
| B、0或9 | ||
C、1或
| ||
| D、1或9 |
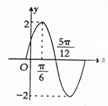 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<