题目内容
集合A={x|x2-2x=0}B={-1，0，1}，则A∩B=（ ）
| A、{0，2} | B、{2} |
| C、{0} | D、{0，1} |
考点：交集及其运算
专题：集合
分析：求出A中方程的解得到x的值，确定出A，找出两集合的交集即可．
解答：
解：由A中的方程变形得：x（x-2）=0，
解得：x=0或x=2，即A={0，2}，
∵B={-1，0，1}，
∴A∩B={0}，
故选：C．
解得：x=0或x=2，即A={0，2}，
∵B={-1，0，1}，
∴A∩B={0}，
故选：C．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如果实数x，y满足条件
，则z=2x-y的最大值为（ ）
|
| A、-3 | B、-1 | C、0 | D、1 |
执行如图所示的程序框图，若输出的n=5，则输入整数P的最小值是（ ）
| A、7 | B、8 | C、15 | D、16 |
在△ABC中，E、F分别为AB、AC中点，P为EF的中点，实数x、y满足
+x
+y
=
，则2x+y的值为（ ）
| PA |
| PB |
| PC |
| 0 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
已知公差不为零的等差数列{an}的首项是公差的4倍，若am是a1和a2m的等比例中项，则m=（ ）
| A、2 | B、3 | C、4 | D、5 |
已知各项都是正数的等比数列{an}中，若a3是6a1与4a2的等差中项，则
=（ ）
| a4+a7 |
| a4+a5 |
| A、7 | ||
| B、9 | ||
C、
| ||
D、
|
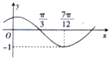函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知tanα=-
，且α为第四象限角，则cosα等于（ ）
| 3 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|