题目内容
已知二次函数f（x）=ax2+bx+c，其中abc＜0，则函数图象可能是（ ）
A、 |
B、 |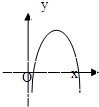
C、 |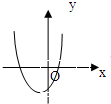
D、 |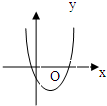
考点：二次函数的性质
专题：函数的性质及应用
分析：根据函数的图象及性质，分别将A，B，C，D四个选项中的a，b，c的符号读出，看是否满足abc＜0即可．
解答：
解；对于选项A：a＜0，b＜0，c＞0，不合题意，
对于选项B：a＜0，b＞0，c＜0，不合题意，
对于选项D：a＞0，b＜0，c＜0，不合题意，
故选：C．
对于选项B：a＜0，b＞0，c＜0，不合题意，
对于选项D：a＞0，b＜0，c＜0，不合题意，
故选：C．
点评：本题考察了二次函数的图象及性质，考察学生的读图能力，是一道基础题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
执行如图所示的程序框图，若输出的n=5，则输入整数P的最小值是（ ）
| A、7 | B、8 | C、15 | D、16 |
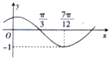函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={1，3，m}，B={1，
}，A∩B=B，那么m=（ ）
| m |
A、0或
| ||
| B、0或9 | ||
C、1或
| ||
| D、1或9 |
如图，E、F、G、H分别是任意四边形ABCD各边中点，若|| AB |
| BC |
| BA |
| AD |
| A、正方形 | B、梯形 | C、菱形 | D、矩形 |
定义在实数集R函数f（x）满足f（x）+f（x+2）=0，且f（x-1）为奇函数，现有以下三种叙述：
（1）8是函数f（x）的一个周期；
（2）f（x）的图象关于点（3，0）对称；
（3）f（x）是偶函数．
其中正确的是（ ）
（1）8是函数f（x）的一个周期；
（2）f（x）的图象关于点（3，0）对称；
（3）f（x）是偶函数．
其中正确的是（ ）
| A、（2）（3） |
| B、（1）（2） |
| C、（1）（3） |
| D、（1）（2）（3） |
已知tanα=-
，且α为第四象限角，则cosα等于（ ）
| 3 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
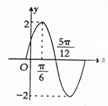已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜