题目内容
已知集合M={x|
＞0}，N={x|x≤-3}，则{x|x≥1}等于（ ）
| x+3 |
| 1-x |
| A、（∁RM）∩N |
| B、M∪（∁RN） |
| C、∁R（M∩N） |
| D、∁R（M∪N） |
考点：交、并、补集的混合运算
专题：集合
分析：求出M中不等式的解集确定出M，求出M与N的并集，找出并集的补集即为所求．
解答：
解：由M中的不等式变形得：
＜0，
解得：-3＜x＜1，即M={x|-3＜x＜1}，
∵N={x|x≤-3}，
∴M∪N={x|x＜1}，
则∁R（M∪N）={x|x≥1}．
故选：D．
| x+3 |
| x-1 |
解得：-3＜x＜1，即M={x|-3＜x＜1}，
∵N={x|x≤-3}，
∴M∪N={x|x＜1}，
则∁R（M∪N）={x|x≥1}．
故选：D．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
在△ABC中，E、F分别为AB、AC中点，P为EF的中点，实数x、y满足
+x
+y
=
，则2x+y的值为（ ）
| PA |
| PB |
| PC |
| 0 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
已知各项都是正数的等比数列{an}中，若a3是6a1与4a2的等差中项，则
=（ ）
| a4+a7 |
| a4+a5 |
| A、7 | ||
| B、9 | ||
C、
| ||
D、
|
函数f（x）=
的零点个数为（ ）
| (x+1)ln(x2-5x+5) | ||
|
| A、3 | B、2 | C、1 | D、0 |
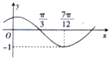函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知变量x，y满足约束条件
，则z=3x+y的取值范围是（ ）
|
| A、[3，11] |
| B、[-1，11] |
| C、[-1，9] |
| D、[-1，3] |
如图，E、F、G、H分别是任意四边形ABCD各边中点，若|| AB |
| BC |
| BA |
| AD |
| A、正方形 | B、梯形 | C、菱形 | D、矩形 |