题目内容
已知两个双曲线
-
=1和
-
=1(a>0,b>0)的渐近线将第一象限三等分,则双曲线
-
=1的离心率( )
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| a2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、2或
| ||||||
B、
| ||||||
C、2或
| ||||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意双曲线
-
=1的渐近线的倾斜角为30°或60°,可得k=
=
或
,利用e=
=
,即可得出结论.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| 3 |
| ||
| 3 |
| c |
| a |
1+(
|
解答:
解:由题意双曲线
-
=1的渐近线的倾斜角为30°或60°,
∴k=
=
或
,
∴e=
=
=2或
,
故选:C.
| x2 |
| a2 |
| y2 |
| b2 |
∴k=
| b |
| a |
| 3 |
| ||
| 3 |
∴e=
| c |
| a |
1+(
|
2
| ||
| 3 |
故选:C.
点评:本题考查双曲线的离心率,确定双曲线
-
=1的渐近线的倾斜角为30°或60°是关键.
| x2 |
| a2 |
| y2 |
| b2 |

练习册系列答案
相关题目
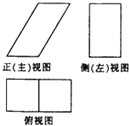 一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为
一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
 某多面体的三视图如图所示,则此多面体的体积为( )
某多面体的三视图如图所示,则此多面体的体积为( )| A、6 | B、9 | C、12 | D、18 |
在区间(0,
)上随机取一个数x,则事件“tanx•cosx>
”发生的概率为( )
| π |
| 2 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知回归直线方程
=
+
x,如果x=3时,y的估计值是17,x=8时,y的估计值是22,那么回归直线方程是( )
 |
| y |
 |
| a |
 |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,则f(x)( )
|
| A、是奇函数但不是偶函数 |
| B、是偶函数但不是奇函数 |
| C、既是奇函数也是偶函数 |
| D、既不是奇函数也不是偶函数 |