题目内容
 如图直四棱柱ABCD-A1B1C1D1中侧棱AA1=
如图直四棱柱ABCD-A1B1C1D1中侧棱AA1=| 6 |
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:求出三棱柱C-PBDD1的体积,减去三棱锥C-PBO与三棱锥C-ODD1的体积,然后求出三棱锥P-ACD1的体积.
解答:
解:∵直四棱柱ABCD-A1B1C1D1中侧棱AA1=
,底面ABCD是棱形,AB=2,∠ABC=60°,
∴AC⊥BD,
∴AC⊥平面PBDD1,
∴VC-POD1=VC-PBDD1-VC-PBO +VC-ODD1=
×
×2
×1-
×
×
×
×1-
×
×
×
×1=
,
所求三棱锥P-ACD1的体积为:2
.
| 6 |
∴AC⊥BD,
∴AC⊥平面PBDD1,
∴VC-POD1=VC-PBDD1-VC-PBO +VC-ODD1=
| 1 |
| 3 |
| ||||||
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 6 |
| 2 |
所求三棱锥P-ACD1的体积为:2
| 2 |
点评:本题考查二面角大小求解,考查空间想象、推理论证能力.考查转化思想以及计算能力.

练习册系列答案
相关题目
 如图给出的是计算1+
如图给出的是计算1+| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 39 |
| A、n=n+2,i>21? |
| B、n=n+2,i>20? |
| C、n=n+1,i≥20? |
| D、n=n+1,i>21? |
 设F是椭圆E:
设F是椭圆E: 已知正方体ABCD-A1B1C1D1的棱长为2a,点E为棱CC1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2a,点E为棱CC1的中点.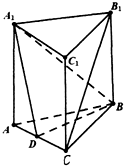 在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC中点.
在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC中点.