题目内容
1.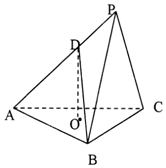 三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.(I)求证:DO∥平面PBC;
(II)求证:AC⊥平面OBD;
(III)求三棱锥B-PDC的体积.
分析 (I)延长AO交BC于E,连结PE,于是$\frac{AD}{DP}=\frac{AO}{OE}$,故而DO∥PE,从而得出DO∥平面PBC;
(II)由面面垂直的性质可得PE⊥平面ABC,得出PE⊥AC,于是DO⊥AC,结合AC⊥OB得出AC⊥平面ODB;
(III)根据面面垂直得出AE⊥平面PBC,从而得出D到平面PBC的距离,代入棱锥的体积公式计算即可.
解答 证明:(I)延长AO交BC于E,连结PE.
∵O是等边ABC的中心,
∴AO=2OE,又∵AD=2DP,
∴OD∥PE,又∵OD?平面PBC,PE?平面PBC,
∴DO∥平面PBC.
(II)∵O是等边三角形ABC的中心,OA∩BC=E,
∴OB⊥AC,E是BC的中点,又∵PB=PC,
∴PE⊥BC.
∵平面PBC⊥平面ABC,平面PBC∩平面ABC=BC,PE⊥BC,PE?平面PBC,
∴PE⊥平面ABC,∵AC?平面ABC,
∴PE⊥AC,又PE∥DO,
∴DO⊥AC,
又DO?平面ODB,OB?平面ODB,OD∩OB=O,
∴AC⊥平面ODB.
(III)∵AE⊥BC,平面PBC⊥平面ABC,平面PBC∩平面ABC=BC,AE?平面ABC,
∴AE⊥平面PBC,
∵O是等边三角形ABC的中心,
∴AE=$\frac{3}{2}$,
∵AD=2DP,
∴D到平面PBC的距离h=$\frac{1}{3}$AE=$\frac{1}{2}$,
∵△PBC是边长为$\sqrt{3}$的等边三角形,
∴S△PBC=$\frac{\sqrt{3}}{4}×3$=$\frac{3\sqrt{3}}{4}$,
∴VB-PDC=VD-PBC=$\frac{1}{3}{S}_{△PBC}•h$=$\frac{1}{3}×\frac{3\sqrt{3}}{4}×\frac{1}{2}$=$\frac{\sqrt{3}}{8}$.
点评 本题考查了线面垂直、线面平行的判定,面面垂直的性质,棱锥的体积计算,属于中档题.

| A. | (-2,0)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
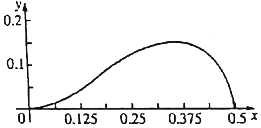 函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )
函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )| A. | m=1,n=1 | B. | m=1,n=2 | C. | m=2,n=3 | D. | m=3,n=1 |
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{3}{7}$ | D. | 2 |
| A. | $[1-\sqrt{3},+∞)$ | B. | [-2,+∞) | C. | $[-2,2\sqrt{2}]$ | D. | $[-2,1+\sqrt{3}]$ |
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | b>c>a |
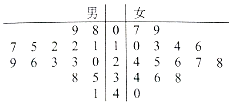 某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.