题目内容
9.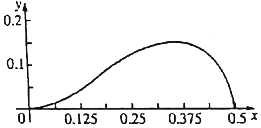 函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )
函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )| A. | m=1,n=1 | B. | m=1,n=2 | C. | m=2,n=3 | D. | m=3,n=1 |
分析 由图得,原函数的极大值点约为0.375.把选项代入验证看哪个对应的极大值点符合要求即可得出答案.
解答 解:由于本题是选择题,可以用代入法来作,
由图得,原函数的极大值点约为0.375.
当m=1,n=1时,f(x)=ax(1-2x)=-2a(x-$\frac{1}{4}$)2+$\frac{a}{8}$.在x=$\frac{1}{4}$处有极大值,故A错误;
当m=1,n=2时,f(x)=axm(1-2x)n=ax(1-2x)2=a(4x3-4x2+x),
所以f′(x)=a(2x-1)(6x-1),a>0,令f′(x)=0⇒x=$\frac{1}{2}$,x=$\frac{1}{6}$,
即函数在x=$\frac{1}{6}$处有极大值,故B错误;
当m=2,n=3时,f(x)=axm(1-2x)n=ax2(1-2x)3,有f'(x)=a(1-2x)2(2x-10x2),
令f′(x)=0⇒x=0,x=$\frac{1}{5}$,x=$\frac{1}{2}$,即函数在x=$\frac{1}{5}$处有极大值,故C错误;
当m=3,n=1时,f(x)=axm(1-2x)n=ax3(1-2x)=a(x3-2x4),
有f′(x)=ax2(3-8x),令f′(x)=0,⇒x=0,x=$\frac{3}{8}$,即函数在x=$\frac{3}{8}$处有极大值,故D正确.
故选:D.
点评 本题主要考查函数的最值(极值)点与导函数之间的关系.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.本题考查利用极值求对应变量的值.可导函数的极值点一定是导数为0的点,但导数为0的点不一定是极值点.

| A. | -$\frac{{a}^{2}}{2}$ | B. | $\frac{{a}^{2}}{2}$ | C. | -2a2 | D. | a2 |
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
| A. | 2+i | B. | 2-i | C. | 5-i | D. | 5+i |
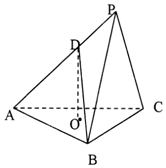 三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.