题目内容
11.a=20.5,b=logπ3,c=log2sin$\frac{2π}{5}$,则( )| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | b>c>a |
分析 利用对数函数、指数函数的单调性求解.
解答 解:∵a=20.5>20=1,
0=logπ1<b=logπ3<logππ=1,
c=log2sin$\frac{2π}{5}$<log21=0,
∴a>b>c.
故选:B.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意对数函数、指数函数的单调性的合理运用.

练习册系列答案
相关题目
2.下面四个条件中,使a>b成立的必要而不充分条件是( )
| A. | a-1>b | B. | a+1>b | C. | |a|>|b| | D. | a3>b3 |
19.若复数z满足(z-3)(2-i)=5(i为虚数单位),则z的共轭复数$\overline{z}$为( )
| A. | 2+i | B. | 2-i | C. | 5-i | D. | 5+i |
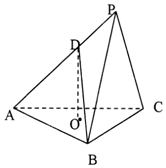 三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
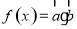 ,其中向量
,其中向量 ,
,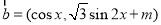 .
.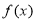 的最小正周期和
的最小正周期和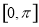 上的单调递增区间;
上的单调递增区间; 时,
时,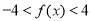 恒成立,求实数
恒成立,求实数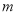 的取值范围.
的取值范围.