题目内容
6.对于函数f(x),若在定义域内存在实数x0,满足f(-x0)=-f(x0),则称f(x)为“局部奇函数”,已知f(x)=4x-m2x+1+m-3为定义R上的“局部奇函数”,则实数m的取值范围是( )| A. | $[1-\sqrt{3},+∞)$ | B. | [-2,+∞) | C. | $[-2,2\sqrt{2}]$ | D. | $[-2,1+\sqrt{3}]$ |
分析 根据“局部奇函数”,可知函数f(-x)=-f(x)有解即可,结合指数函数的性质,利用换元法进行求解.
解答 解:根据“局部奇函数”的定义可知,函数f(-x)=-f(x)有解即可,
即f(-x)=4-x-m•2-x+1+m-3=-(4x-m2x+1+m-3),
∴4x+4-x-2m(2x+2-x)+2m-6=0,
即(2x+2-x)2-2m?(2x+2-x)+2m-8=0有解即可.
设t=2x+2-x,则t=2x+2-x≥2,
∴方程等价为t2-2m?t+2m-8=0在t≥2时有解,
则g(t)=t2-2m?t+2m-8,其对称轴为t=m,
①若m≥2,有△=4m2-4(2m-8)=4(m2-2m+8)≥0恒成立,
即m≥4时,满足题意,
②若m<4,要使t2-2m?t+2m-8=0在t≥2时有解,
令g(t)=t2-2m?t+2m-8,
则有$\left\{\begin{array}{l}{m<2}\\{△≥0}\\{g(2)≤0}\end{array}\right.$
解得-2≤m<2,
综上:m≥-2,即m的取值范围是[2,+∞);
故选:B.
点评 本题主要考查函数的新定义,利用函数的新定义得到方程有解的条件,利用换元法将方程转化为一元二次方程有解的问题去解决是解决本题的关键.综合考查了二次函数的图象和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.过点P(1,1)且倾斜角为45°的直线被圆(x-2)2+(y-1)2=2所截的弦长是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
18.已知等比数列{an}满足a1+a3=10,a2+a4=5,则a5=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
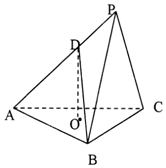 三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.