题目内容
16.过点P(1,2)的直线l与圆(x-3)2+(y-1)2=5相切,若直线ax+y+3=0与直线l垂直,则a=( )| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{3}{7}$ | D. | 2 |
分析 求出点P在圆上,圆(x-3)2+(y-1)2=5的圆心C(3,1),从而kPC=-$\frac{1}{2}$,进而直线l的斜率k=-$\frac{1}{{k}_{PC}}$=2,再由直线ax+y+3=0与直线l垂直,能求出a的值.
解答 解:把P(1,2)代入圆(x-3)2+(y-1)2=5,得(1-3)2+(2-1)2=5,
∴点P在圆上,
圆(x-3)2+(y-1)2=5的圆心C(3,1),
∵过点P(1,2)的直线l与圆(x-3)2+(y-1)2=5相切,
${k}_{PC}=\frac{1-2}{3-1}$=-$\frac{1}{2}$,
∴直线l的斜率k=-$\frac{1}{{k}_{PC}}$=2,
∵直线ax+y+3=0与直线l垂直,
∴-a•2=-1,解得a=$\frac{1}{2}$.
故选:B.
点评 本题考查实数值的求法,考查圆、直线方程、斜率公式、直线与直线垂直的条件、直线与圆相切等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是中档题.

练习册系列答案
相关题目
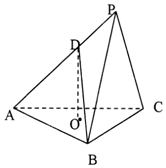 三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.