题目内容
下列有关命题的说法正确的是（ ）
| A、若p∧q为假命题，则p，q均为假命题 |
| B、命题“若x=y，则sinx=siny”为真命题 |
| C、命题“?x0∈R，使得x02+x0+1＜0”的否定是：“?x∈R，均有x2+x+1＜0” |
| D、“x2=1”是“x=-1”的充分不必要条件 |
考点：命题的真假判断与应用
专题：简易逻辑
分析：A．根据或命题的意义即可判断出；
B．根据三角函数的定义可以判断出；
C．根据命题的否定的意义即可判断出；
D．根据充要条件的定义，可判断出．
B．根据三角函数的定义可以判断出；
C．根据命题的否定的意义即可判断出；
D．根据充要条件的定义，可判断出．
解答：
解：对于A，若p∧q为假命题，则p，q中存在至少一个假命题，但不一定p，q均为假命题，故错误；
对于B，若x=y，则sinx=siny为真命题，故正确；
对于C，命题“?x0∈R，使得x02+x0+1＜0”的否定是：“?x∈R，均有x2+x+1≥0”，故错误；
对于D，“x2=1”是“x=-1”的必要不充分条件，故错误；
故选：B
对于B，若x=y，则sinx=siny为真命题，故正确；
对于C，命题“?x0∈R，使得x02+x0+1＜0”的否定是：“?x∈R，均有x2+x+1≥0”，故错误；
对于D，“x2=1”是“x=-1”的必要不充分条件，故错误；
故选：B
点评：本题考查了四种命题之间的关系、命题的否定，属于基础题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
设函数f（x）=3x+bcosx，x∈R，则“b=0”是“函数f（x）为奇函数”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
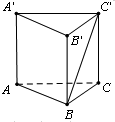如图所示，在底面为正三角形的三棱柱ABC-A1B1C1中，若AA1⊥平面ABC，AB=| 2 |
| A、60° | B、45° |
| C、90° | D、120° |
已知函数y=f（x）满足f（π-x）=f（x），且当x∈（-
，
）时，f（x）=xsinx-cosx，则（ ）
| π |
| 2 |
| π |
| 2 |
| A、f（2）＜f（3）＜f（4） |
| B、f（3）＜f（4）＜f（2） |
| C、f（4）＜f（3）＜f（2） |
| D、f（4）＜f（2）＜f（3） |