题目内容
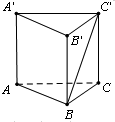 如图所示,在底面为正三角形的三棱柱ABC-A1B1C1中,若AA1⊥平面ABC,AB=
如图所示,在底面为正三角形的三棱柱ABC-A1B1C1中,若AA1⊥平面ABC,AB=| 2 |
| A、60° | B、45° |
| C、90° | D、120° |
考点:异面直线及其所成的角
专题:平面向量及应用,空间位置关系与距离,空间角
分析:设BB1=1,则AB=
,将向量分解得
=
+
,
=
+
,结合题意算出数量积
•
=0,得到
⊥
,从而得出异面直线AB1与C1B所成的角的大小为90°.
| 2 |
| AB1 |
| AB |
| BB1 |
| C1B |
| C1C |
| CB |
| AB1 |
| C1B |
| AB1 |
| C1B |
解答:
解:如图,设BB1=1,则AB=
,
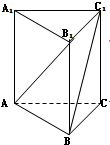
∵正三角形ABC中,∴∠ABC=60°
可得
•
=(
+
)•(
+
)=
•
+
•
+
•
+
•
=0-1+|
|•|
|cos60°+0=-1+
•
cos60°=-1+1=0
因此,
⊥
,
可得异面直线AB1与C1B所成的角的大小为90°
故选:C
| 2 |

∵正三角形ABC中,∴∠ABC=60°
可得
| AB1 |
| C1B |
| AB |
| BB1 |
| C1C |
| CB |
| AB |
| C1C |
| BB1 |
| C1C |
| AB |
| CB |
| BB1 |
| CB |
| AB |
| CB |
| 2 |
| 2 |
因此,
| AB1 |
| C1B |
可得异面直线AB1与C1B所成的角的大小为90°
故选:C
点评:本题给出特殊的正三棱柱,求异面直线所成角的大小.着重考查了正三棱柱的性质、利用空间向量研究异面直线所成角的大小等知识,属于中档题.

练习册系列答案
相关题目
若复数z满足z=(z-1)•i,则复数z的模为( )
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
下列有关命题的说法正确的是( )
| A、若p∧q为假命题,则p,q均为假命题 |
| B、命题“若x=y,则sinx=siny”为真命题 |
| C、命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1<0” |
| D、“x2=1”是“x=-1”的充分不必要条件 |
在△ABC中,如果AB=5,AC=3,BC=4,那么角
•
等于( )
| AB |
| AC |
| A、9 | B、12 | C、15 | D、20 |