题目内容
已知数列{an}是首项a1=1,公差大于0的等差数列,其前n项和为Sn,数列{bn}是首项b1=2的等比数列,且b2S2=16,b3S3=72.
(1)求an和bn;
(2)令c1=1,c2k=a2k-1,c2k+1=a2k+kbk(k=1,2,3,…),求数列{cn}的前2n+1项和T2n+1.
(1)求an和bn;
(2)令c1=1,c2k=a2k-1,c2k+1=a2k+kbk(k=1,2,3,…),求数列{cn}的前2n+1项和T2n+1.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)直接利用等差数列和等比数列建立方程组求出数列的通项公式.
(2)根据构造的新数列的特点,利用乘公比错位相减法和等差数列的前n项和公式求出结果.
(2)根据构造的新数列的特点,利用乘公比错位相减法和等差数列的前n项和公式求出结果.
解答:
解:(1)设数列{an}的公差为d(d>0)数列{bn}的公比为q,
则an=1+(n-1)d,bn=2qn-1.
依题意得b2S2=2q(2+d)=16,b3S3=2q2(3+3d)=72
由此得
∵d>0,解得
.
∴an=2n-1,bn=2n.
(2)∵T2n+1=c1+a1+(a2+b1)+a3+(a4+2•b2)+…+a2n-1+(a2n+nbn)
=1+S2n+(b1+2b2+…+nbn)
令A=b1+2b2+…+nbn
则A=2+2•22+…+n•2n2A
=22+2•23+…+(n-1)2n+n•2n+1-A
=2+22+…+2n-n•2n+1,
∴A=n•2n+1-2n+1+2
又S2n=
=4n2,
∴T2n+1=1+4n2+n•2n+1-2n+1+2
=3+4n2+(n-1)2n+1.
则an=1+(n-1)d,bn=2qn-1.
依题意得b2S2=2q(2+d)=16,b3S3=2q2(3+3d)=72
由此得
|
∵d>0,解得
|
∴an=2n-1,bn=2n.
(2)∵T2n+1=c1+a1+(a2+b1)+a3+(a4+2•b2)+…+a2n-1+(a2n+nbn)
=1+S2n+(b1+2b2+…+nbn)
令A=b1+2b2+…+nbn
则A=2+2•22+…+n•2n2A
=22+2•23+…+(n-1)2n+n•2n+1-A
=2+22+…+2n-n•2n+1,
∴A=n•2n+1-2n+1+2
又S2n=
| 2n(1+a2n) |
| 2 |
∴T2n+1=1+4n2+n•2n+1-2n+1+2
=3+4n2+(n-1)2n+1.
点评:本题考查的知识要点:数列通项公式的求法,乘公比错位相减法的应用,数列前n项和的应用.属于中等题型.

练习册系列答案
相关题目
已知F1,F2分别是双曲线
-
=1的左、右焦点,P为双曲线右支上的任意一点,则
的最小值为( )
| x2 |
| 4 |
| y2 |
| 21 |
| |PF1|2 |
| |PF2| |
| A、24 | B、20 | C、16 | D、12 |
下列有关命题的说法正确的是( )
| A、若p∧q为假命题,则p,q均为假命题 |
| B、命题“若x=y,则sinx=siny”为真命题 |
| C、命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1<0” |
| D、“x2=1”是“x=-1”的充分不必要条件 |
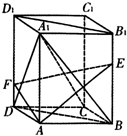 如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.
如图,在长方体A BCD-A1B1C1D1中,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.