题目内容
当x∈（0，1）时，函数y=xk（k∈R）的图象在直线y=x的上方，则k的取值范围是（ ）
| A、（1，+∞） |
| B、（-∞，1） |
| C、（0，1） |
| D、[0，1） |
考点：利用导数求闭区间上函数的最值
专题：函数的性质及应用
分析：由题意，0＜x＜1时，xk＞x，xk-x=x（xk-1-1）＞0，由此能求出k的取值范围．
解答：
解：由题意，0＜x＜1时，xk＞x，
xk-x=x（xk-1-1）＞0
∵x＞0，∴xk-1＞1
∴k-1＜0，k＜1．
∴k的取值范围是（-∞，1）．
故选：B．
xk-x=x（xk-1-1）＞0
∵x＞0，∴xk-1＞1
∴k-1＜0，k＜1．
∴k的取值范围是（-∞，1）．
故选：B．
点评：本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
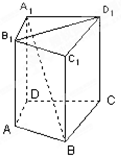如图，在直四棱柱A1B1C1D1-ABCD中，当底面四边形ABCD满足条件