题目内容
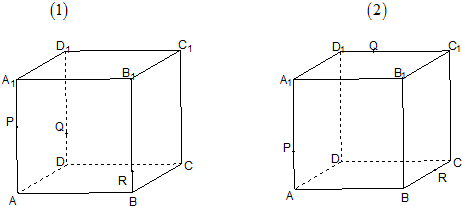
如图，在直四棱柱A1B1C1D1-ABCD中，当底面四边形ABCD满足条件考点：棱柱的结构特征
专题：空间位置关系与距离
分析：根据题意，由A1B⊥B1D1，结合直棱柱的性质，分析底面四边形ABCD，只要BD⊥AC，进而验证即可．
解答：
解：∵四棱柱A1B1C1D1-ABCD是直棱柱，
∴A1D⊥平面A1B1C1D1，
∴B1D1⊥A1D，若A1B⊥B1D1
则B1D1⊥平面A1BD，
∴B1D1⊥BD，
又由B1D1∥AC，
则有BD⊥AC，
反之，由BD⊥AC亦可得到A1B⊥B1D1
故答案为：BD⊥AC．
∴A1D⊥平面A1B1C1D1，
∴B1D1⊥A1D，若A1B⊥B1D1
则B1D1⊥平面A1BD，
∴B1D1⊥BD，
又由B1D1∥AC，
则有BD⊥AC，
反之，由BD⊥AC亦可得到A1B⊥B1D1
故答案为：BD⊥AC．
点评：本题主要考查了棱柱的几何特征以及空间线线，线面，面面垂直关系的转化与应用．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
函数f（x）=（x-3）ex的单调递减区间是（ ）
| A、（-∞，2） |
| B、（0，3） |
| C、（1，4） |
| D、（2，+∞） |
当x∈（0，1）时，函数y=xk（k∈R）的图象在直线y=x的上方，则k的取值范围是（ ）
| A、（1，+∞） |
| B、（-∞，1） |
| C、（0，1） |
| D、[0，1） |
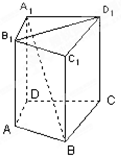
如图，在三棱柱ABC-A1B1C1中，△ABC是边长为2的等边三角形，AA1⊥平面ABC，