题目内容
4.已知f(x)是定义在R上的奇函数,对任意x>0,都有f(x+4)=f(x),若f(-2)=2,则f(2 018)等于( )| A. | 2 012 | B. | 2 | C. | 2 013 | D. | -2 |
分析 根据函数奇偶性和周期性的性质进行转化求解即可.
解答 解:∵对任意x>0,都有f(x+4)=f(x),
∴当x>0时,函数的周期是4,
则f(2 018)=f(4×504+2)=f(2),
∵f(x)是定义在R上的奇函数,若f(-2)=2,
∴f(-2)=-f(2)=2,
则f(2)=-2,
即f(2 018)=f(2 )=-2,
故选:D
点评 本题主要考查函数值的计算,根据函数奇偶性和周期性的性质进行转化是解决本题的关键.

练习册系列答案
相关题目
12.方程lnx+2x-6=0的近似解所在的区间是( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
13.执行如图的程序框图,则输出S的值为( )
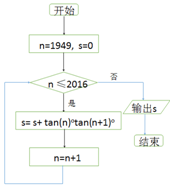

| A. | $\frac{tan2017°-tan1949°}{tan1°}$-67 | B. | $\frac{tan2016°-tan1949°}{tan1°}$-67 | ||
| C. | $\frac{tan2017°-tan1949°}{tan1°}$-68 | D. | $\frac{tan2016°-tan1949°}{tan1°}$-68 |
14.若不等式 $m>n与\frac{1}{m}>\frac{1}{n}(m,n∈R)$ 同时成立,则 ( )
| A. | m>0>n | B. | 0>m>n | ||
| C. | m>n>0 | D. | m,n与0的大小关系不确定 |