题目内容
14.下列四个命题中:①“等边三角形的三个内角均为60°?”的逆命题;
②“若k>0,则方程x2+2x-k=0有实根”的逆否命题;
③“全等三角形的面积相等”的否命题;
④“若ab≠0,则a≠0”的否命题.
其中真命题的个数是①②.
分析 ①,三个内角均为60°的三角形一定是等边三角形;
②,原命题为真,其逆否命题与原命题同真假;
③,不全等三角形的不面积也可以相等;
④,“若ab=0,则a=0或b=0”.
解答 解:对于①“等边三角形的三个内角均为60°”的逆命题:三个内角均为60°的三角形是等边三角形,故为真命题;
对于②,“若k>0,则方程x2+2x-k=0的△=4+4k>0,有实根”,∴原命题为真,其逆否命题与原命题同真假,故为真命题;
对于③,“不全等三角形的面积可以相等”,故其否命题:不全等三角形的不面积相等,故为假命题;
对于 ④,若ab=0,则a=0或b=0”,故为假命题.
故选:D
点评 本题考查了命题的真假判定,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知函数f(x)=x2+2(a-1)x+b在区间(-∞,4]上递减,则a的取值范围是( )
| A. | [-3,+∞) | B. | (-∞,-3] | C. | (-∞,5] | D. | [3,+∞) |
5.在△ABC中,2AB=3AC,∠A=$\frac{π}{3}$,∠BAC的平分线交边BC于点D,|AD|=1,则( )
| A. | AB•AC=$\sqrt{2}$AB+AC | B. | AB+AC=$\sqrt{2}$AB•AC | C. | AB•AC=$\sqrt{3}$AB+AC | D. | AB+AC=$\sqrt{3}$AB•AC |
2.已知集合I,M,N的关系如图所示,则I,M,N的关系为( )
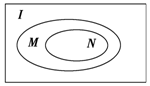

| A. | (∁IM)?(∁IN) | B. | M⊆(∁IN) | C. | (∁IM)⊆(∁IN) | D. | M?(∁IN) |
6.下列有关命题的说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x>1,则$\frac{1}{x}$<1”的逆否命题为真命题 |
4.已知f(x)是定义在R上的奇函数,对任意x>0,都有f(x+4)=f(x),若f(-2)=2,则f(2 018)等于( )
| A. | 2 012 | B. | 2 | C. | 2 013 | D. | -2 |
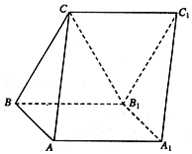 如图,三棱柱ABC-A1B1C1的侧面AA1B1B是边长为2的正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面AA1B1B是边长为2的正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.