题目内容
13.执行如图的程序框图,则输出S的值为( )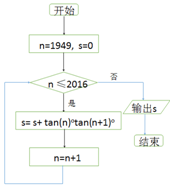
| A. | $\frac{tan2017°-tan1949°}{tan1°}$-67 | B. | $\frac{tan2016°-tan1949°}{tan1°}$-67 | ||
| C. | $\frac{tan2017°-tan1949°}{tan1°}$-68 | D. | $\frac{tan2016°-tan1949°}{tan1°}$-68 |
分析 执行程序框图,得出S的算式,再利用两角差的正切公式计算S的值即可.
解答 解:执行如图的程序框图,知程序运行后计算并输出
S=tan1949°tan1950°+tan1950°tan1951°+…+tan2016°tan2017°,
又S=(1+tan1949°tan1950°)+(1+tan1950°tan1951°)+…+(1+tan2016°tan2017°)-(2017-1950+1)
=$\frac{tan1950°-tan1949°}{tan(1950°-1949°)}$+$\frac{tan1951°-tan1950°}{tan(1951°-1950°)}$+…+$\frac{tan2017°-tan2016°}{tan(2017°-2016°)}$-68
=$\frac{tan2017°-tan1949°}{tan1°}$-68,
所以输出S=$\frac{tan2017°-tan1949°}{tan1°}$-68.
故选:C.
点评 本题主要考查了循环结构与三角函数求值的应用问题,根据流程图写出程序的运行结果,是算法重要的题型,属于综合性题目.

练习册系列答案
相关题目
4.已知f(x)是定义在R上的奇函数,对任意x>0,都有f(x+4)=f(x),若f(-2)=2,则f(2 018)等于( )
| A. | 2 012 | B. | 2 | C. | 2 013 | D. | -2 |
18.对于定义域为R的函数f(x),若存在非零实数x0,使函数f(x)在(-∞,x0)和(x0,+∞)上与x轴均有交点,则称x0为函数f(x)的一个“界点”.则下列四个函数中,不存在“界点”的是( )
| A. | f(x)=x2+bx-2(b∈R) | B. | f(x)=|x2-3| | C. | f(x)=1-|x-2| | D. | f(x)=x3+x |