若不等式 $m＞n与\frac{1}{m}＞\frac{1}{n}$ 同时成立.则 ( )A．m＞0＞nB．0＞m＞nC．m＞n＞0D．m.n与0的大小关系不确定题目和参考答案——青夏教育精英家教网—

题目内容

14．若不等式 $m＞n与\frac{1}{m}＞\frac{1}{n}（m，n∈R）$ 同时成立，则（　　）

	A．	m＞0＞n		B．	0＞m＞n
	C．	m＞n＞0		D．	m，n与0的大小关系不确定

分析由$\frac{1}{m}$$＞\frac{1}{n}$，可得$\frac{m-n}{mn}$＜0，由不等式 $m＞n与\frac{1}{m}＞\frac{1}{n}（m，n∈R）$ 同时成立，利用不等式的基本性质即可判断出结论．

解答解：由$\frac{1}{m}$$＞\frac{1}{n}$，可得$\frac{m-n}{mn}$＜0，
∵不等式 $m＞n与\frac{1}{m}＞\frac{1}{n}（m，n∈R）$ 同时成立，
∴mn＜0，因此m＞0＞n．
故选：A．

点评本题考查了不等式的基本性质，考查了推理能力与计算能力，属于基础题．

练习册系列答案

5．给出下列四个命题：
①两个向量相等，则它们的起点相同，终点相同；
②若$\overrightarrow{a}$=$\overrightarrow{b}$，$\overrightarrow{b}$=$\overrightarrow{c}$，则$\overrightarrow{a}$=$\overrightarrow{c}$；
③设$\overrightarrow{{a}_{0}}$是单位向量，若$\overrightarrow{d}$∥$\overrightarrow{{a}_{0}}$，且|$\overrightarrow{d}$|=1，则$\overrightarrow{d}$=$\overrightarrow{{a}_{0}}$；
④$\overrightarrow{d}$=$\overrightarrow{b}$的充要条件是|$\overrightarrow{d}$=|$\overrightarrow{b}$|且$\overrightarrow{d}$∥$\overrightarrow{b}$．
其中假命题的个数为（　　）

2．已知正三棱锥P-ABC，点P，A，B，C都在半径为$\sqrt{2}$的球面上，若PA，PB，PC两两相互垂直，则球心到截面ABC的距离为$\frac{\sqrt{2}}{3}$．

9．已知曲线 f（x）=ax²-2在横坐标为1的点 p处切线的倾斜角为$\frac{π}{4}$，则a=（　　）

19．椭圆$C：{x^2}+\frac{y^2}{4}=1$的焦点坐标是（0，±$\sqrt{3}$）；长轴长为4．

6．

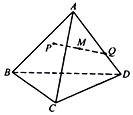如图，在三棱锥A-BCD中，AB⊥AD，AC⊥AD，∠BAC=60°，AB=AC=AD=4，点P，Q分别在侧面ABC棱AD上运动，PQ=2，M为线段PQ中点，当P，Q运动时，点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于$\frac{π}{{48\sqrt{3}-π}}$．

3．已知命题p：?x＞1，x²-2x+1＞0，则￢p是假命题（真命题/假命题）．

17．已知P：?x∈Z，x³＜1，则￢P是（　　）

试题分类