题目内容
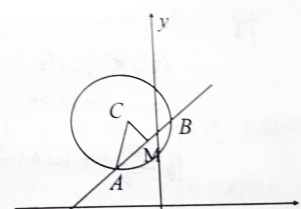
在极坐标系中,已知圆ρ=3cosθ与直线2ρcosθ+4ρsinθ+a=0相切,求实数a的值.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把圆与直线的极坐标方程分别化为直角坐标方程,再利用直线与圆相切的性质可得:圆心到直线的距离等于半径即可解出.
解答:
解:由圆ρ=3cosθ,可得ρ2=3ρcosθ,化为直角坐标方程:x2+y2=3x,
配方为(x-
)2+y2=
,圆心为C(
,0),半径r=
.
直线2ρcosθ+4ρsinθ+a=0化为直角坐标方程:2x+4y+a=0.
∵直线与圆相切可得:
=
,解得a=-3±3
.
配方为(x-
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
直线2ρcosθ+4ρsinθ+a=0化为直角坐标方程:2x+4y+a=0.
∵直线与圆相切可得:
|
| ||
|
| 3 |
| 2 |
| 5 |
点评:本题考查了极坐标方程化为直角坐标方程、直线与圆相切的性质、点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
总体容量为102,现用系统抽样法抽样,若剔除了2个个体,则抽样间隔可以是( )
| A、7 | B、8 | C、9 | D、10 |