题目内容
A与B比赛,若一队胜四场则赢,俩队水平相当.
求:(1)A队一、五场输,二、三、四赢,最后获胜的概率
(2)若要决出胜负,平均要比几场?
求:(1)A队一、五场输,二、三、四赢,最后获胜的概率
(2)若要决出胜负,平均要比几场?
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)分别求出A队第六场赢的概率和A队第六场输且第七场赢的概率,相加,即得所求.
(2)设ξ为比赛场数,则ξ可能取值为4,5,6,7,求出ξ取每个值的概率,再代入随机变量的数学期望的计算公式,可得ξ的数学期望,即为所求.
(2)设ξ为比赛场数,则ξ可能取值为4,5,6,7,求出ξ取每个值的概率,再代入随机变量的数学期望的计算公式,可得ξ的数学期望,即为所求.
解答:
解:(1)A队若第六场赢,概率为P1=
•(
)3•
•
=
=
,
A队若第六场输,第七场赢,概率为P2=
•(
)3•(
)2•
=
=
,
∴A队最终获胜的概率为
+
=
.
(2)设ξ为比赛场数,则ξ可能取值为4,5,6,7,
P(ξ=4)=2•(
)4=
,P(ξ=5)=2
•(
)3•
•
=
,
P(ξ=6)=2
•(
)3•(
)2•
=
,P(ξ=7)=2
•(
)3•(
)3•
=
,
Eξ=4×
+5×
=6×
+7×
≈6,∴平均需比赛约6场.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 26 |
| 1 |
| 64 |
A队若第六场输,第七场赢,概率为P2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 27 |
| 1 |
| 128 |
∴A队最终获胜的概率为
| 1 |
| 64 |
| 1 |
| 128 |
| 3 |
| 128 |
(2)设ξ为比赛场数,则ξ可能取值为4,5,6,7,
P(ξ=4)=2•(
| 1 |
| 2 |
| 1 |
| 8 |
| C | 3 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
P(ξ=6)=2
| C | 3 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 16 |
| C | 3 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 16 |
Eξ=4×
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 16 |
| 5 |
| 16 |
点评:本题主要考查相互独立事件的概率乘法公式,n次独立重复实验中恰好发生k次的概率,求随机变量的数学期望,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
位于坐标原点的一个支点P按下述规则移动:质点每次移动一个单位:移动的方向为向上或向右,并且向上、向右移动的概率都是0.5,质点P移动6次后位于点(2,4)的概率为( )
A、(
| ||||||
B、C
| ||||||
C、C
| ||||||
D、C
|
若直线y=k(x+4)与曲线x=
有交点,则k的取值范围是( )
| 4-y2 |
A、[-
| ||||||||
B、(-∞,-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
已知a,b是实数,则“lga>lgb”是“(
)a<(
)b”的( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
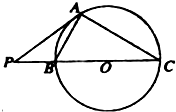 如图,已知直线 P A切圆 O于点 A,直线 P O交圆 O于点 B、C,若PC=2+
如图,已知直线 P A切圆 O于点 A,直线 P O交圆 O于点 B、C,若PC=2+