题目内容
已知不等式|x-2|>1的解集与关于x的不等式x2-ax+b>0的解集相等.
(Ⅰ)求实数a,b的值;
(Ⅱ)求函数f(x)=a
+b
的最大值,以及取得最大值时x的值.
(Ⅰ)求实数a,b的值;
(Ⅱ)求函数f(x)=a
| x-3 |
| 5-x |
考点:柯西不等式在函数极值中的应用,一元二次不等式的解法,绝对值不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)由绝对值不等式的解法,可得解集为{x|x<1或x>3},进而得到1,3为方程x2-ax+b=0的两根,代入方程即可得到a,b;
(Ⅱ)运用柯西不等式,可得f(x)的最大值,同时由等号成立的条件可得x的值.
(Ⅱ)运用柯西不等式,可得f(x)的最大值,同时由等号成立的条件可得x的值.
解答:
解:(Ⅰ)∵不等式|x-2|>1的解集为{x|x<1或x>3},
∴不等式x2-ax+b>0的解集为{x|x<1或x>3}.
从而1,3为方程x2-ax+b=0的两根,
∴
,
解得:a=4,b=3.
(Ⅱ)函数f(x)的定义域为[3,5],且显然有y>0,
由柯西不等式可得:
y=4
+3
≤
×
=5
,
当且仅当:4
=3
时等号成立,
即x=
时,函数取得最大值5
.
∴不等式x2-ax+b>0的解集为{x|x<1或x>3}.
从而1,3为方程x2-ax+b=0的两根,
∴
|
解得:a=4,b=3.
(Ⅱ)函数f(x)的定义域为[3,5],且显然有y>0,
由柯西不等式可得:
y=4
| x-3 |
| 5-x |
| 42+32 |
(
|
| 2 |
当且仅当:4
| 5-x |
| x-3 |
即x=
| 107 |
| 25 |
| 2 |
点评:本题考查绝对值不等式和二次不等式的解法,考查柯西不等式的运用:求最值,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
“四边形ABCD为菱形”是“四边形ABCD中AC=BD”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设抛物线C1:y2=2x与双曲线C2:
-
=1的焦点重合,且双曲线C2的渐近线为y=±
x,则双曲线C2的实轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
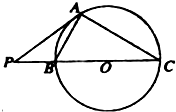 如图,已知直线 P A切圆 O于点 A,直线 P O交圆 O于点 B、C,若PC=2+
如图,已知直线 P A切圆 O于点 A,直线 P O交圆 O于点 B、C,若PC=2+