题目内容
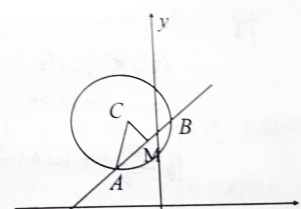
已知点P(0,5),圆C:x2+y2+4x-12y+24=0,过P点的直线l与圆C相交于A,B两点.
(1)若弦AB的长为4
,求直线l的方程
(2)若弦AB的长有最小值时,求直线l的方程.

(1)若弦AB的长为4
| 3 |
(2)若弦AB的长有最小值时,求直线l的方程.
考点:直线与圆的位置关系
专题:综合题,直线与圆
分析:(1)求圆C的方程:x2+y2+4x-12y+24=0,我们可以求出圆心C的坐标和圆的半径r,结合直线l被圆C截得的线段AB长,代入圆的弦长公式,可得弦心距d,再由点到直线距离公式,可求出直线l的斜率,由直线l过点P,可得直线的点斜式方程.解答时要注意直线l的斜率不存在时,也满足题意.
(2)弦AB的长有最小值时,CP⊥AB,求出斜率,即可求直线l的方程.
(2)弦AB的长有最小值时,CP⊥AB,求出斜率,即可求直线l的方程.
解答:
解:(1)由已知得(x+2)2+(y-6)2=16
∴圆C的圆心C(-2,6),半径为4.
由已知|AB|=4
,|AC|=4
设D是线段AB的中点,则CD⊥AB,
∴|AD|=2
,
在Rt△ACD中,可得|CD|=2.
设所求直线l的斜率为k,则直线l的方程为:y-5=kx,
即kx-y+5=0.由点C到直线AB的距离公式:
=2,得k=
,…
此时直线l的方程为3x-4y+20=0.
又直线l的斜率不存在时,也满足题意,此时方程为x=0.
∴所求直线l的方程为x=0或3x-4y+20=0.
(2)弦AB的长有最小值时,CP⊥AB,
∵kCP=-
,∴kAB=2,
∴弦AB的长有最小值时,直线l的方程为y=2x+5.
∴圆C的圆心C(-2,6),半径为4.
由已知|AB|=4
| 3 |
设D是线段AB的中点,则CD⊥AB,
∴|AD|=2
| 3 |
在Rt△ACD中,可得|CD|=2.
设所求直线l的斜率为k,则直线l的方程为:y-5=kx,
即kx-y+5=0.由点C到直线AB的距离公式:
| |-2k-6+5| | ||
|
| 3 |
| 4 |
此时直线l的方程为3x-4y+20=0.
又直线l的斜率不存在时,也满足题意,此时方程为x=0.
∴所求直线l的方程为x=0或3x-4y+20=0.
(2)弦AB的长有最小值时,CP⊥AB,
∵kCP=-
| 1 |
| 2 |
∴弦AB的长有最小值时,直线l的方程为y=2x+5.
点评:本题考查的知识点是直线与圆的位置关系,求直线的方程,求圆的方程,属于中档题.

练习册系列答案
相关题目
已知a>0,b>0,且2a+b=1,则
+
的最小值为( )
| 2 |
| a |
| 1 |
| b |
| A、7 | B、8 | C、9 | D、10 |
“四边形ABCD为菱形”是“四边形ABCD中AC=BD”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设抛物线C1:y2=2x与双曲线C2:
-
=1的焦点重合,且双曲线C2的渐近线为y=±
x,则双曲线C2的实轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=ax+xa(a>0),则下列说法正确的是( )
| A、?a>0,f(x)为偶函数,且在R上单调递增 |
| B、?a>0,f(x)-1为奇函数,且在R上单调递增 |
| C、?a>0,f(x)为奇函数,且在R上单调递减 |
| D、?a>0,f(x)-1为偶函数,且在R上单调递减 |