题目内容
已知0<x<
,求函数f(x)=2x(1-2x)的最大值.
| 1 |
| 2 |
考点:二次函数在闭区间上的最值
专题:计算题,不等式的解法及应用
分析:确定1-2x>0,利用f(x)=2x(1-2x)≤(
)2,即可求函数f(x)=2x(1-2x)的最大值.
| 2x+1-2x |
| 2 |
解答:
解:∵0<x<
,
∴0<2x<1,
∴1-2x>0,
∴f(x)=2x(1-2x)≤(
)2=
,
当且仅当2x=1-2x,即x=
时,函数f(x)=2x(1-2x)的最大值为
.
| 1 |
| 2 |
∴0<2x<1,
∴1-2x>0,
∴f(x)=2x(1-2x)≤(
| 2x+1-2x |
| 2 |
| 1 |
| 4 |
当且仅当2x=1-2x,即x=
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题考查函数的最大值的求法,是基础题,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知4a+b=1(a,b>0),则
+
的最小值为( )
| 1 |
| a |
| 4 |
| b |
| A、8 | B、12 | C、16 | D、20 |
已知f(x)=x2+bx+c,且f(1)=f(3)=0,则f(x)的单调递减区间为( )
| A、(-∞,1)或(3 ,+∞) |
| B、(1,3) |
| C、(-∞,2) |
| D、(2,+∞) |
已知实数x,y满足约束条件
则z=x+3y的最大值等于( )
|
| A、9 | B、0 | C、27 | D、36 |
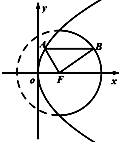 已知△ABF,点F(2,0),点A,B分别在图中抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△ABF的周长的取值范围是
已知△ABF,点F(2,0),点A,B分别在图中抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△ABF的周长的取值范围是