题目内容
已知集合A={x|x2-4x-5≤0},B={x2-2x-m<0}.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
考点:交、并、补集的混合运算,交集及其运算
专题:不等式的解法及应用,集合
分析:(1)把m=3代入不等式,分别求解一元二次不等式化简集合A,B,然后利用补集与交集运算求解;
(2)由集合A结合A∩B={x|-1<x<4}可知4∈B,把x=4代入方程x2-2x-m=0求得m的值.
(2)由集合A结合A∩B={x|-1<x<4}可知4∈B,把x=4代入方程x2-2x-m=0求得m的值.
解答:
解:(1)由x2-4x-5≤0,得(x+1)(x-5)≤0,
解得:-1≤x≤5.
∴A={x|x2-4x-5≤0}={x|-1≤x≤5},
当m=3时,B={x2-2x-m<0}={x2-2x-3<0},
由x2-2x-3<0,得(x+1)(x-3)<0.
解得-1<x<3.
∴B={x|-1<x<3},
则∁RB={x|x≤-1或x≥3}
∴A∩(∁RB)={x|3≤x≤5或x=-1};
(2)∵A={x|-1≤x≤5},
A∩B={x|-1<x<4},
∴42-2×4-m=0,解得m=8,
此时B={x|-2<x<4},符合题意,
故实数m的值为8.
解得:-1≤x≤5.
∴A={x|x2-4x-5≤0}={x|-1≤x≤5},
当m=3时,B={x2-2x-m<0}={x2-2x-3<0},
由x2-2x-3<0,得(x+1)(x-3)<0.
解得-1<x<3.
∴B={x|-1<x<3},
则∁RB={x|x≤-1或x≥3}
∴A∩(∁RB)={x|3≤x≤5或x=-1};
(2)∵A={x|-1≤x≤5},
A∩B={x|-1<x<4},
∴42-2×4-m=0,解得m=8,
此时B={x|-2<x<4},符合题意,
故实数m的值为8.
点评:本题考查了交、并、补集的混合运算,考查了数学转化思想方法,关键是对题意的理解,是中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
已知等差数列{an}的前n项和Sn,满足Sn=-
n2+2n,则Sn的最大值为( )
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
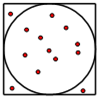 某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为39粒,则由此估计出的圆周率π的值为
某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为39粒,则由此估计出的圆周率π的值为