题目内容
已知椭圆的两焦点F1、F2，点P在椭圆上，且PF1⊥PF2，已知|PF1|=3，|F1F2|=5，试建立适当的坐标系求出椭圆的标准方程．
考点：椭圆的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：以F1F2所在直线为x轴，F1F2垂直平分线为y轴，建立坐标系，求出a，b，即可得出椭圆的方程．
解答：
解：以F1F2所在直线为x轴，F1F2垂直平分线为y轴，建立坐标系，则c=2.5，
∵PF1⊥PF2，|PF1|=3，|F1F2|=5，
∴|PF2|=4，
∴2a=7，
∴a=3.5，
∴b=
，
∴椭圆的标准方程为
+
=1．
∵PF1⊥PF2，|PF1|=3，|F1F2|=5，
∴|PF2|=4，
∴2a=7，
∴a=3.5，
∴b=
| 6 |
∴椭圆的标准方程为
| x2 |
| 12.25 |
| y2 |
| 6 |
点评：本题考查椭圆的标准方程，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
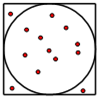某同学动手做实验：《用随机模拟的方法估计圆周率的值》，在如图的正方形中随机撒豆子，每个豆子落在正方形内任何一点是等可能的，若他随机地撒50粒统计得到落在圆内的豆子数为39粒，则由此估计出的圆周率π的值为