题目内容
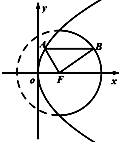已知△ABF，点F（2，0），点A，B分别在图中抛物线y2=8x及圆（x-2）2+y2=16的实线部分上运动，且AB总是平行于x轴，则△ABF的周长的取值范围是考点：圆与圆锥曲线的综合
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：由抛物线定义可得|AF|=xA+2，从而△FAB的周长=|AF|+|AB|+|BF|=xA+2+（xB-xA）+4=6+xB，确定B点横坐标的范围，即可得到结论．
解答：
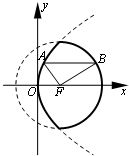解：抛物线的准线l：x=-2，焦点F（2，0），
由抛物线定义可得|AF|=xA+2，
圆（x-2）2+y2=16的圆心为（2，0），半径为4，
∴△FAB的周长=|AF|+|AB|+|BF|=xA+2+（xB-xA）+4=6+xB，
由抛物线y2=8x及圆（x-2）2+y2=16可得交点的横坐标为2，
∴xB∈（2，6）
∴6+xB∈（8，12）
故答案为：（8，12）
解：抛物线的准线l：x=-2，焦点F（2，0），由抛物线定义可得|AF|=xA+2，
圆（x-2）2+y2=16的圆心为（2，0），半径为4，
∴△FAB的周长=|AF|+|AB|+|BF|=xA+2+（xB-xA）+4=6+xB，
由抛物线y2=8x及圆（x-2）2+y2=16可得交点的横坐标为2，
∴xB∈（2，6）
∴6+xB∈（8，12）
故答案为：（8，12）
点评：本题考查抛物线的定义，考查抛物线与圆的位置关系，确定B点横坐标的范围是关键．
练习册系列答案
相关题目