题目内容
已知f（x）=x2+bx+c，且f（1）=f（3）=0，则f（x）的单调递减区间为（ ）
| A、（-∞，1）或（3 ，+∞） |
| B、（1，3） |
| C、（-∞，2） |
| D、（2，+∞） |
考点：二次函数的性质
专题：函数的性质及应用
分析：根据f（1）=f（3）=0可求出b，从而求出f（x）的对称轴，根据二次函数的单调性即可写出f（x）的单调递减区间．
解答：
解：由已知条件得：
，解得b=-4；
所以函数f（x）的对称轴是：x=2；
∴f（x）的单调递减区间为（-∞，2）．
故选C．
|
所以函数f（x）的对称轴是：x=2；
∴f（x）的单调递减区间为（-∞，2）．
故选C．
点评：考查二次函数的对称轴，二次函数的单调性．
练习册系列答案
阅读快车系列答案
相关题目
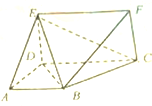如图所示，直角梯形ABCD和矩形CDEF所在的平面互相垂直，AD⊥DC，AB∥DC，AB=AD=DE=1，CD=2．