题目内容
函数f（x）=4x3+k•
+1（k∈R），若f（2）=8，则f（-2）的值为 ．
| 3 | x |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：由f（x）=4x3+k•
+1得f（x）-1=4x3+k•
为奇函数，然后利用奇函数的性质即可得到结论．
| 3 | x |
| 3 | x |
解答：
解：∵f（x）=4x3+k•
+1，
∴f（x）-1=4x3+k•
，则f（x）-1为奇函数，
∴f（-2）-1=-[f（2）-1]，
即f（-2）=-f（2）+1+1=-8+2=-6，
故答案为：-6．
| 3 | x |
∴f（x）-1=4x3+k•
| 3 | x |
∴f（-2）-1=-[f（2）-1]，
即f（-2）=-f（2）+1+1=-8+2=-6，
故答案为：-6．
点评：本题主要考查函数值的计算，利用条件构造函数f（x）-1，利用函数的奇偶性是解决本题的关键，本题也可以直接解方程进行求解．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
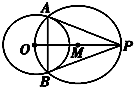如图，已知P为⊙O外一点，以PO为直径作⊙M，⊙M交⊙O于A、B两点，求证：PA、PB是⊙O的切线．与
=(-3，4)共线的单位向量是（ ）
| a |
A、（-
| ||||||||
B、（
| ||||||||
C、（-
| ||||||||
D、（
|