题目内容
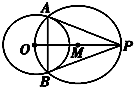如图，已知P为⊙O外一点，以PO为直径作⊙M，⊙M交⊙O于A、B两点，求证：PA、PB是⊙O的切线．考点：圆的切线方程
专题：证明题,选作题
分析：连接OA，OB，利用A是以PO为直径的⊙M上一点，可得∠PAO=90°，根据切线的判定定理，即可得证．
解答：
证明：连接OA，OB，
∵A是以PO为直径的⊙M上一点，
∴∠PAO=90°，
根据切线的判定定理，可知PA是⊙O的切线．
同理PB是⊙O的切线．
证明：连接OA，OB，∵A是以PO为直径的⊙M上一点，
∴∠PAO=90°，
根据切线的判定定理，可知PA是⊙O的切线．
同理PB是⊙O的切线．
点评：本题考查圆的切线，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
复数z=
的虚部是（ ）
| -3+i |
| 2+i |
| A、1 | B、-i | C、i | D、-1 |
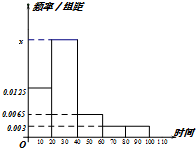某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．
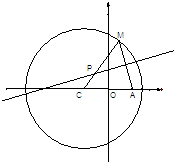如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P是线段AM的垂直平分线与直线CM的交点．