题目内容
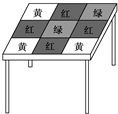一张方桌的图案如图所示，将一颗豆子随机地扔到桌面上，假设豆子不落在线上，下列事件的概率（1）豆子落在红色区域概率为
| 4 |
| 9 |
（2）豆子落在黄色区域概率为
| 1 |
| 3 |
（3）豆子落在绿色区域概率为
| 2 |
| 9 |
（4）豆子落在红色或绿色区域概率为
| 1 |
| 3 |
（5）豆子落在黄色或绿色区域概率为
| 4 |
| 9 |
其中正确的结论有（ ）
| A、2个 | B、3个 | C、4个 | D、5个 |
考点：命题的真假判断与应用
专题：概率与统计
分析：由图可知：桌面等分成9部分，把每一部分看作一个基本事件，其基本事件的总数为9．其中红色区域包括4个基本事件，黄色区域包括3个基本事件，绿色区域包括2个基本事件．利用古典概型的概率计算公式即可得出．
解答：
解：由图可知：桌面等分成9部分，把每一部分看作一个基本事件，其基本事件的总数为9．其中红色区域包括4个基本事件，黄色区域包括3个基本事件，绿色区域包括2个基本事件．
∴（1）豆子落在红色区域概率P=
，因此正确；
（2）豆子落在黄色区域概率P=
=
，因此正确；
（3）豆子落在绿色区域概率P=
，因此正确；
（4）利用互斥事件的概率计算公式可得：豆子落在红色或绿色区域概率P=
+
=
，因此不正确；
（5）同理：豆子落在黄色或绿色区域概率=
+
=
，因此不正确．
综上可知：正确的只有（1）（2）（3）．
故选：B．
∴（1）豆子落在红色区域概率P=
| 4 |
| 9 |
（2）豆子落在黄色区域概率P=
| 3 |
| 9 |
| 1 |
| 3 |
（3）豆子落在绿色区域概率P=
| 2 |
| 9 |
（4）利用互斥事件的概率计算公式可得：豆子落在红色或绿色区域概率P=
| 4 |
| 9 |
| 2 |
| 9 |
| 2 |
| 3 |
（5）同理：豆子落在黄色或绿色区域概率=
| 3 |
| 9 |
| 2 |
| 9 |
| 5 |
| 9 |
综上可知：正确的只有（1）（2）（3）．
故选：B．
点评：本题考查了古典概型的概率计算公式和互斥事件的概率计算公式，属于基础题．
练习册系列答案
相关题目
数列{an}的通项公式为an=2n+4n-2，则数列{an}的前n项和sn=（ ）
| A、2n+2n2-1 |
| B、2n+2n2-2 |
| C、2n+1+2n2-1 |
| D、2n+1+2n2-2 |
设点（a，b）是区域
内的随机点，函数f（x）=ax2-4bx+1在区间[1，+∞）上是增函数的概率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
设x、y满足约束条件
，若x2+y2≥a恒成立，则实数a的最大值为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
学校为了调查学生在课外读物方面的支出情况，将支出分区间[20，30）、[30，40）、[40，50）、[50，60）进行统计，现抽出了一个容量为n的样本，其频率分布直方图如图所示，其中支出在[50，60）元的同学有24人，则n的值为（ ）