题目内容
若x、y满足条件
,则z=x+3y的最大值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,利用利用数形结合即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:
由z=x+3y,得y=-
x+

平移直线y=-
x+
,由图象可知当y=-
x+
,经过点C时,直线截距最大,此时z最大.
由
得
,即A(2,3),
此时z=x+3y=2+3×3=11,
故答案为:11.
由z=x+3y,得y=-
| 1 |
| 3 |
| z |
| 3 |

平移直线y=-
| 1 |
| 3 |
| z |
| 3 |
| 1 |
| 3 |
| z |
| 3 |
由
|
|
此时z=x+3y=2+3×3=11,
故答案为:11.
点评:本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
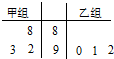 甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机挑选一名同学,则这两名同学成绩相同的概率是
甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机挑选一名同学,则这两名同学成绩相同的概率是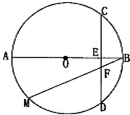 如图,AB为半径为2的圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦BM与CD交于点F.则AC2+BF•BM=
如图,AB为半径为2的圆O的直径,CD为垂直于AB的一条弦,垂足为E,弦BM与CD交于点F.则AC2+BF•BM=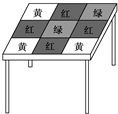 一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率
一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率