题目内容
设点(a,b)是区域
内的随机点,函数f(x)=ax2-4bx+1在区间[1,+∞)上是增函数的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型,简单线性规划
专题:概率与统计
分析:作出不等式组对应的平面区域,根据概率的几何概型的概率公式进行计算即可得到结论.
解答:
解:作出不等式组
对应的平面区域如图:对应的图形为△OAB,其中对应面积为S=
×4×4=8,
若f(x)=ax2-4bx+1在区间[1,+∞)上是增函数,
则满足a>0且对称轴x=-
=
≤1,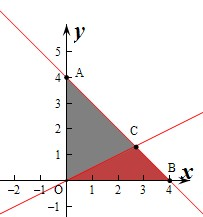
即
,对应的平面区域为△OBC,
由
,
解得
,
∴对应的面积为S 1=
×4×
=
,
∴根据几何概型的概率公式可知所求的概率为
=
,
故选:C
|
| 1 |
| 2 |
若f(x)=ax2-4bx+1在区间[1,+∞)上是增函数,
则满足a>0且对称轴x=-
| -4b |
| 2a |
| 2b |
| a |

即
|
由
|
解得
|
∴对应的面积为S 1=
| 1 |
| 2 |
| 4 |
| 3 |
| 8 |
| 3 |
∴根据几何概型的概率公式可知所求的概率为
| ||
| 8 |
| 1 |
| 3 |
故选:C
点评:本题主要考查几何概型的概率公式的计算,作出不等式组对应的平面区域是解决本题的关键.

练习册系列答案
相关题目
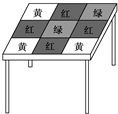 一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率
一张方桌的图案如图所示,将一颗豆子随机地扔到桌面上,假设豆子不落在线上,下列事件的概率(1)豆子落在红色区域概率为
| 4 |
| 9 |
(2)豆子落在黄色区域概率为
| 1 |
| 3 |
(3)豆子落在绿色区域概率为
| 2 |
| 9 |
(4)豆子落在红色或绿色区域概率为
| 1 |
| 3 |
(5)豆子落在黄色或绿色区域概率为
| 4 |
| 9 |
其中正确的结论有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
已知O为坐标原点,P1、P2是双曲线
-
=1上的点.P是线段P1P2的中点,直线OP、P1P2的斜率分别为k1、k2,若2≤k1≤4,则k2的取值范围是( )
| x2 |
| 9 |
| y2 |
| 4 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知x,y满足约束条件
,则目标函数z=2x-3y的最大值( )
|
| A、2 | B、3 | C、4 | D、5 |
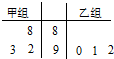 甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机挑选一名同学,则这两名同学成绩相同的概率是
甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机挑选一名同学,则这两名同学成绩相同的概率是 某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为
某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为