题目内容
已知O是△ABC所在平面内一定点,动点P满足
=
+λ(
sinB+
sinC)(λ≥0),则P点的轨迹一定通过△ABC的( )
| OP |
| OA |
| AB |
| AC |
| A、内心 | B、外心 | C、垂心 | D、重心 |
考点:轨迹方程
专题:平面向量及应用
分析:作AD⊥BC,可以得出|
|sinB=|
|sinC=|
|,由此对已知条件变形即可得出结论.
| AB |
| AC |
| AD |
解答:
解:如图,

作AD⊥BC,由于|
|sinB=|
|sinC=|
|,
∴
=
+λ(
sinB+
sinC)=
+λ(
•
+
•
)
=
+λ|
|(
+
).
即
=λ|
|(
+
).
由加法法则知,P在三角形的角分线上,
故动点P的轨迹一定通过△ABC的内心.
故选:A.

作AD⊥BC,由于|
| AB |
| AC |
| AD |
∴
| OP |
| OA |
| AB |
| AC |
| OA |
| AB |
|
| ||
|
|
| AC |
|
| ||
|
|
=
| OA |
| AD |
| ||
|
|
| ||
|
|
即
| AP |
| AD |
| ||
|
|
| ||
|
|
由加法法则知,P在三角形的角分线上,
故动点P的轨迹一定通过△ABC的内心.
故选:A.
点评:本题考点是三角形的五心,考查了五心中内心的几何特征以及向量的加法与数乘运算,解答本题的关键是理解向量加法的几何意义,从而确定点的几何位置,是中档题.

练习册系列答案
相关题目
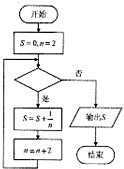 阅读如图所示的程序框图,运行相应的程序,若输出的S为
阅读如图所示的程序框图,运行相应的程序,若输出的S为| 11 |
| 12 |
| A、n=6 | B、n<6 |
| C、n≤6 | D、n≤8 |
从长度为1、3、5、7、9个单位的五条线段中任取三条作边,能组成三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若x、y满足不等式组
,则
的最小值是( )
|
| x2+y2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
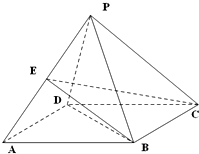 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=